L N в электрике — цвета проводов в трехжильном кабеле
В подавляющем большинстве кабелей разная расцветка изоляции жил. Сделано это в соответствие с ГОСТом Р 50462-2009, который устанавливает стандарт маркировки l n в электрике (фазных и нулевых проводов в электроустановках). Соблюдения этого правила гарантирует быструю и безопасную работу мастера на большом промышленном объекте, а также позволяет избежать электротравм при самостоятельном ремонте.
Разнообразие расцветки изоляции электрокабелей
Цветовая маркировка проводов многообразна и сильно различается для заземления, фазных и нулевых жил. Чтобы не было путаницы, требования ПУЭ регламентируют какого цвета провод заземления использовать в щитке электропитания, какие расцветки обязательно надо использовать для нуля и фазы.
Если монтажные работы проводились высококвалифицированным электриком, который знает современные стандарты работы с электропроводами, не придется прибегать к помощи индикаторной отвёртки или мультиметра. Назначение каждой жилы кабеля расшифровывается знанием его цветового обозначения.
Назначение каждой жилы кабеля расшифровывается знанием его цветового обозначения.
Цвет жилы заземления
С 01.01.2011 цвет жилы заземления (или зануления) может быть только желто-зеленой. Эта цветовая маркировка проводов соблюдается и при составлении схем, на которых такие жилы подписываются латинскими буквами РЕ. Не всегда на кабелях расцветка одной из жил предназначена для заземления – обычно она делается если в кабеле три, пять или больше жил.
Отдельного внимания заслуживают PEN-провода с совмещенными «землей» и «нолем». Подключения такого типа все еще часто встречаются в старых зданиях, в которых электрификация проводилась по устаревшим нормам и до сих пор не обновлялась. Если кабель укладывался по правилам, то использовался синий цвет изоляции, а на кончики и места стыков надевались желто-зеленые кембрики. Хотя, можно встретить и цвет провода заземления (зануления) с точностью до наоборот – желто-зеленый с синими кончиками.
Заземляющая и нулевая жила могут отличаются толщиной, часто она тоньше фазных, особенно на кабелях, что применяются для подключения переносных устройств.
Защитное заземление является обязательным при прокладке линий в жилых и промышленных помещениях и регулируется стандартами ПУЭ и ГОСТ 18714-81. Провод нулевой заземляющий должен иметь как можно меньшее сопротивление, то же самое касается заземляющего контура. Если все работы по монтажу выполнено правильно, то заземление будет надежным защитником жизни и здоровья человека в случае появления неисправностей электролинии. Как итог – правильная пометка кабелей для заземления имеет решающее значение, а зануление вообще не должно применяться. Во всех новых домах проводка делается по новым правилам, а старые поставлены в очередь для ее замены.
Расцветки для нулевого провода
Для «ноля» (или нулевого рабочего контакта) используются только определенные цвета проводов также строго определяемые электрическими стандартами. Он может быть синим, голубым или синим с белой полоской, причем независимо от количества жил в кабеле: трехжильный провод в этом плане ничем не будет отличаться от пятижильного или с еще большим количеством проводников. В электросхемах «нулю» соответствует латинская буква N – он участвует в замыкании цепи электропитания, а в схемах может читаться как «минус» (фаза, соответственно, это «плюс»).
В электросхемах «нулю» соответствует латинская буква N – он участвует в замыкании цепи электропитания, а в схемах может читаться как «минус» (фаза, соответственно, это «плюс»).
Цвета для фазных проводов
Эти электропровода требуют особо осторожного и «уважительного» с собой обращения, так как они являются токоведущими, и неосторожное прикосновение может вызвать тяжелое поражение электрическим током. Цветовая маркировка проводов для подключения фазы достаточно разнообразна – нельзя применять только цвета смежные с синим, желтым и зеленым. В какой-то мере так гораздо удобнее запоминать каким может быть цвет провода фазы – НЕ синим или голубым, НЕ желтым или зеленым.
На электросхемах фазу обозначают латинской буквой L. Такая же разметка используется на проводах, если цветовая маркировка ни них не применяется. Если кабель предназначен для подключения трех фаз, то фазные жилы помечают буквой L с цифрой. Например, для составления схемы для трехфазной сети 380 В использовано L1, L2, L3. Еще в электрике принято альтернативное обозначение: A, B, C.
Еще в электрике принято альтернативное обозначение: A, B, C.
Настоятельно рекомендуется использовать одинаковую расцветку проводов, при ответвлении однофазной цепи от трехфазной.
Перед началом работ надо определиться, как будет выглядеть комбинация проводов по цвету и неукоснительно придерживаться выбранной расцветки.
Если этот вопрос был продуман еще на этапе подготовительных работ и учтен при составлении схем электропроводки, следует закупить необходимое количество кабелей с жилами необходимых цветов. Если все-таки нужный провод закончился, то можно пометить жилы вручную:
- кембриками обычными;
- кембриками термоусадочными;
- изолентой.
О стандартах цветовой маркировки проводов в Европе и России смотрите так же в этом видео:
Ручная цветовая разметка
Применяется в тех случаях, когда при монтаже приходится использовать провода с жилами одинаковой расцветки. Также часто это происходит при работе в домах старой постройки, в которых монтаж электропроводки производился задолго до появления стандартов.
Также часто это происходит при работе в домах старой постройки, в которых монтаж электропроводки производился задолго до появления стандартов.
Опытные электрики, чтобы не было путаницы при дальнейшем обслуживании электроцепи использовали наборы, позволяющие промаркировать фазные провода. Это допускается и современными правилами, ведь некоторые кабели изготавливаются без цветобуквенных обозначений. Место использования ручной маркировки регламентировано нормами ПУЭ, ГОСТа и общепринятыми рекомендациями. Она крепится на концы проводника, там, где он соединяется с шиной.
Разметка двужильных проводов
Если кабель уже подключен к сети, то для поиска фазных проводов в электрике используют специальную индикаторную отвертку – в ее корпусе есть светодиод, который светится, когда жало устройства касается фазы.
Правда эффективной она будет только для двухжильных проводов, ведь если фаз несколько, то определить где какая индикатор не сможет. В таком случае придется отключать провода и использовать прозвонку.
Далее понадобится набор специальных трубок с термоусадочным эффектом или ленты для изоляции, чтобы разметить фазу и ноль.
Стандарты не обязывают делать такую разметку на электропроводниках по всей их длине. Допускается отметить её лишь в местах стыков и соединения нужных контактов. Поэтому, при возникновении необходимости нанести метки на электрокабели без обозначений, нужно заранее приобрести материалы, для их разметки вручную.
Число используемых расцветок зависит от применяемой схемы, но главная рекомендация все же есть – желательно использовать цвета, исключающие возможность путаницы. Т.е. не применять для фазных проводов синие, желтые или зеленые метки. В однофазной сети, к примеру, фазу обычно обозначают красным цветом.
Разметка трехжильных проводов
Если надо определить фазу, ноль и заземление в трехжильных проводах, то можно попробовать сделать это мультиметром. Прибор устанавливается на измерение переменного напряжения, а затем щупами аккуратно коснуться фазы (его можно найти и индикаторной отверткой) и последовательно двух оставшихся проводов.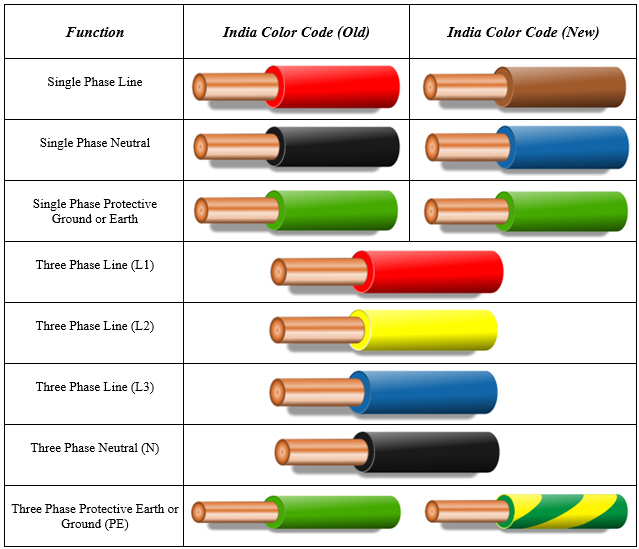 Далее следует запомнить показатели и сравнить их между собой – комбинация «фаза-ноль» обычно показывает большее напряжение, нежели «фаза-земля».
Далее следует запомнить показатели и сравнить их между собой – комбинация «фаза-ноль» обычно показывает большее напряжение, нежели «фаза-земля».
Когда фаза, ноль и земля определены, то можно наносить маркировку. По правилам, для заземления применяется провод цветной желто зеленый, а точнее жила с такой расцветкой, поэтому его маркируют изолентой подходящих цветов. Ноль, отмечается, соответственно, синей изолентой, а фаза любой другой.
Если же при профилактических работах выяснилось, что маркировка устарела, менять кабеля не обязательно. Замене, в соответствии с современными стандартами, подлежит только электрооборудование, вышедшее из строя.
Как итог
Правильная разметка проводов это обязательное условие качественного монтажа электропроводки при проведении работ любой сложности. Она значительно облегчает как сам монтаж, так и последующее обслуживание электросети. Чтобы электрики «разговаривали на одном языке», созданы обязательные стандарты цветобуквенной маркировки, которые схожи между собой даже в разных странах. В соответствии с ними L – это обозначение фазы, а N – ноля.
В соответствии с ними L – это обозначение фазы, а N – ноля.
различение цветовой маркировки и ее использование на практике
Большинство изделий кабельно-проводниковой продукции имеют цветовое отличие изоляции жил, называемое «маркировкой», играющее важную роль в практическом применении. Правильное использование маркировки значительно облегчает работу персонала по обслуживанию электрических сетей, позволяя быстро определять нужные проводники и производить их коммутацию в электроустановках. Окраска проводников осуществляется в соответствии с ПУЭ и каждый электрик должен быть ознакомлен с ней для обеспечения безопасности, как личной, так и людей, которые будут работать в дальнейшем. Читайте также статью ⇒ Особенности конструкций проводов, кабелей и шнуров, критерии выбора.
Основные цвета изоляции жил в бытовых электросетях
В бытовом использовании наиболее часто встречаются двух- или трехжильные провода. Основная их масса с двойной изоляцией имеет различия жил по цвету. Правилами устройства электроустановок предусмотрены следующие отличия:
Правилами устройства электроустановок предусмотрены следующие отличия:
- «земля» (на схемах обозначается, как РЕ-проводник) – окрашивается чередующимися желтыми и зелеными полосами, реже, в некоторых кабельных изделиях — чисто желтым или чисто зеленым цветом;
- «ноль» или «нейтраль» (на изображениях схем подписывается латинской буквой «N») – имеет синий, бело-синий или голубой окрас;
- «фаза» (именуется на электросхемах литерой «L») – может иметь любой другой цвет (даже фиолетовый), но чаще всего бывает белым, черным или коричневым.
Нужно знать, что в описаниях схем земля может называться «защитным нулем», а ноль — «рабочим нулем». Эти понятия нельзя путать, потому что они имеют абсолютно различные значения. Не менее важным условием является умение отличать проводники друг от друга.
Жила заземления обеспечивает защиту человека от поражения током на случай повреждения изоляции и утечки электричества на корпус прибора, находящегося под напряжением. В процессе подачи электроэнергии она не играет никакой роли. В отличие от нее, нулевой проводник является неотъемлемой частью электрической цепи, и при подключении нагрузки обтекается током.
В процессе подачи электроэнергии она не играет никакой роли. В отличие от нее, нулевой проводник является неотъемлемой частью электрической цепи, и при подключении нагрузки обтекается током.
Распределение по цвету фазных, нулевых и заземляющих проводов согласно ПУЭ
При проведении коммутации, синие провода соединяются между собой, либо подключаются к контакту электроприбора «N». Фазные провода направляются к контакту «L». Заземляющие жилы коммутируются с клеммой, имеющей соответствующее обозначение:
Условное обозначение контакта заземления на схемах и корпусах электроприборов
Кабеля трехфазных цепей могут иметь цвет силовых жил желтый, зеленый и красный/черный. Цвет заземляющей и нулевой жилы при этом остается неизменным – желто-зеленым и синим соответственно. Необходимо быть внимательным, чтобы на перепутать двухцветный проводник со схожим одноцветным.
Маркировка проводов сетей постоянного тока обычно производится красным «+» и черным «-» цветом.
Определение назначения жил на одноцветных проводах
Иногда изоляционные оболочки провода не имеют цветовых различий. Обычно это изделия с однослойной изоляцией типа ППВ или АППВ. Для простоты ориентирования следует знать и принять за правило, что в качестве заземляющего проводника всегда используется средняя жила. «Фазу» и «ноль» определяют с помощью индикатора напряжения (индикаторной отвертки).
Обычно это изделия с однослойной изоляцией типа ППВ или АППВ. Для простоты ориентирования следует знать и принять за правило, что в качестве заземляющего проводника всегда используется средняя жила. «Фазу» и «ноль» определяют с помощью индикатора напряжения (индикаторной отвертки).
Определение земли, фазы и нуля на одноцветном трехжильном проводе
Определить «ноль» и «землю» можно также с помощью тестера мультиметра. При его установке на измерение напряжения и замыкании щупов между фазой и «0» на дисплее отобразится значение напряжения близкое к 220 В. При контакте с заземляющим проводом показания будут немного выше.
Еще одним способом различения нейтральной и заземляющей жилы является использование омметра. Его показания сопротивления на заземлении не должны превышать 4 Ом.
Важным моментом является правило: измерение напряжения производится при наличии электричества, а сопротивления – при его отсутствии.
Самостоятельная маркировка проводов
В случае отсутствия цветовых различий на изоляции жил провода или кабеля, их маркировку можно осуществить своими руками для удобства последующей эксплуатации. Это делается двумя способами:
Это делается двумя способами:
- с помощью цветной изоляционной ленты;
- с применением разноцветных ПВХ кембриков или термоусадочных трубок.
Обычно обозначаются концы провода в местах их коммутации между собой или с клеммами потребителей электроэнергии согласно описанным выше принципам маркировки (фаза, ноль, земля). Изолента наматывается в один-два витка и держится на жилах за счет своей клейкости, а термоусадочная трубка после надевания на провод подвергается воздействию высокой температуры, в результате чего плотно обжимает его.
Цветные кембрики для производства маркировки проводов своими руками
Эти материалы рекомендуется использовать и для изоляции холодных счалок между жилами, что поможет в дальнейшем избежать путаницы.
Практическая рекомендация: Обозначение фазы и нейтрали в распределительных коробках можно осуществить также с помощью цветных соединительных изолирующих зажимов, одетых на проводные скрутки.
Использование цветовой маркировки на практике
Умение отличить «фазу» по цвету изоляции, может пригодиться при установке защитного устройства, например, автоматического выключателя.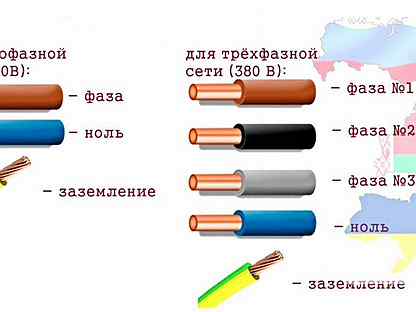 Пользователь без труда определит проводник «L», на который нужно поставить защиту.
Пользователь без труда определит проводник «L», на который нужно поставить защиту.
Во время подключения розетки, знание цвета проводов согласно ПУЭ, поможет безошибочно отличить жилу заземления и произвести ее коммутацию с соответствующей клеммой. Эти же навыки пригодятся при сборке разъема (вилки).
Использование маркированных проводов при подключении люстры или осветительной сети на несколько линий даст возможность без проведения «прозвонки» осуществить подсоединение выключателя и произвести электрическую разводку, направив к каждому светильнику свою цветную линию.
Схема осветительной сети на две линии с цветовым обозначением проводов
Знание маркировки жил кабеля во многом помогает при ремонте электрического оборудования, как в быту, так и на производственных объектах. У грамотного электрика не возникнет вопроса, какого цвета провод соединить с заземляющим контактом или с «рабочим нулем».
Однако следует помнить, что быть уверенным в соблюдении правил маркировки жил кабеля можно только в тех случаях, если их подключение производилось лично или на заводе изготовителе. На незнакомых объектах перед началом работы необходимо убедиться в правильности цветовой коммутации.
На незнакомых объектах перед началом работы необходимо убедиться в правильности цветовой коммутации.
Различия в цветовых обозначениях некоторых зарубежных стран
Большинство стран мира, включая Европу и США, приняли схожие правила маркировки проводов. Так, например, заземляющие жилы имеют желто-зеленую или чисто зеленую оболочку. Иногда «земля» не покрывается изоляцией вовсе.
Нулевые жилы помимо синего колера могут иметь черную, белую или серую (серебристый металлик) окраску, а фазные жилы в большинстве случаев покрываются яркими цветными оболочками.
Для сравнения, цветовая маркировка кабелей иностранных государств приведена в таблице:
| Государство | Фазные проводники | Рабочий ноль | Защитный ноль |
| Аргентина | Черный, коричневый, серый | Синий | Желто-зеленый |
| Бразилия | Желтый, красный, черный, белый | Синий | Зеленый |
| США, Канада | Красный, желтый, коричневый, синий, черный | Белый, серебристый металлик | Зеленый, желто-зеленый, голый |
| Евросоюз | Коричневый, черный, серый | Синий | Желто-зеленый |
| Индия, Пакистан | Красный, желтый, синий | Черный | Зеленый, желто-зеленый |
| ЮАР | Красный, белый, желтый, синий | Черный | Желто-зеленый |
| Австралия, Новая Зеландия | Коричневый, белый, красный, желтый | Черный, синий | Зеленый, желто-зеленый, голый |
Указанные в таблице расцветки фазных токоведущих жил являются основными и общепризнанными. Могут встречаться и другие цвета, но это больше исключение, чем правило.
Могут встречаться и другие цвета, но это больше исключение, чем правило.
Распространенные ошибки при пользовании цветовой маркировкой
Большинство ошибок, совершаемых при подключении или соединении проводов, являются следствием невнимательного отношения к цветовой маркировке жил или ее игнорирования. Среди наиболее часто допускаемых недочетов стоит отметить следующие:
- Обустройство электрической проводки без предварительного ознакомления с правилами ПУЭ, в результате чего подключение жил производится без учета соответствия цвета жил их назначению. Следствием этого может стать путаница в обслуживании электрических сетей и сложности при осуществлении их ремонта другим специалистом
- Подключение по невнимательности к клемме заземления токоведущего провода, имеющего схожую окраску (например, бирюзовую). Результатом станет аварийное срабатывание защитного устройства (отключение автоматического выключателя), либо короткое замыкание, способное привести к выходу оборудования из строя
- Использование на скрутках в распределительной коробке соединительных изолирующих пластиковых колпачков (СИЗ) несоответствующего цвета.
 Это может ввести в заблуждение обслуживающий персонал, который будет проводить ремонт или ревизию электропроводки
Это может ввести в заблуждение обслуживающий персонал, который будет проводить ремонт или ревизию электропроводки
Соединительные изолирующие зажимы (СИЗ) для защиты скруток в распределительных коробках
- Удаление РЕ проводника при установке розетки, не имеющей заземляющих контактов. Это грубая ошибка, посягающая на безопасность при использовании электроэнергии. Вместо удаления заземляющей жилы лучше поменять устаревшую розетку на изделие, соответствующее современным стандартам
- Ошибка может быть допущена и при соблюдении цветовых маркировочных обозначений. Например, если провести счалку в виде скрутки между медным и алюминиевым проводником, то контакт будет ненадежным, хотя цвета оболочек будут совпадать
Внимательное отношение к требованиям нормативных документов и соблюдение техники безопасности поможет избежать ошибок при обслуживании электрических сетей и обезопасить их эксплуатацию.
Актуальные вопросы по теме
Вопрос: Что делать если при обустройстве домашней электропроводки используется провод с несоответствующей цветовой маркировкой жил, или вообще не имеющий ее?
Ответ: Можно отметить имеющиеся цвета и их подключение в своей памяти, но лучше произвести самостоятельную маркировку, как это указано в 3-м разделе данной статьи.
Вопрос: Не является ли нарушением использование проводника с желто-зеленой изоляцией в системе уравнивания потенциалов (СУП)?
Ответ: Это не может быть нарушением, потому что данная система является разновидностью заземления корпусов мощных электроприборов, поэтому цвет жилы должен соответствовать назначению.
Вопрос: Можно ли при самостоятельной прокладке РЕ проводника в доме, где он не предусмотрен электропроводкой, использовать обычный провод, а потом маркировать его?
Ответ: Конечно можно. Единственное условие – произвести маркировку во всех, без исключения, местах подключения, чтобы избежать путаницы при дальнейшей эксплуатации.
Вопрос: Если в розетке отсутствуют обозначения «L» и «N» значит ли это, что подключение проводов можно производить произвольно, без учета цвета оболочки жил?
Ответ: Да, в таких розетках не имеет значения, куда подключать «ноль» и «фазу», но нужно проконтролировать правильное подключение «земли» и установку защитных устройств строго на фазный провод.
В заключении можно отметить, что цветовая маркировка проводов имеет большое значение не только в практическом отношении, но и в вопросах безопасности. Поэтому каждому пользователю, сталкивающемуся с вопросами обслуживания электросетей, будет полезно ознакомиться с принципами обозначения проводников цветом и использовать полученные знания на практике. Читайте также статью: → «Провода для электропроводки».
Оцените качество статьи:
Цвета проводов в электрике
Каждый раз, когда я устанавливаю розетку или подключаю какой-то стационарный прибор встаёт вопрос о том, что значит цвет провода — фаза? Или это земля? Неразберихи добавляет то, что далеко не все кабеля — это наши родные ВВГ-3 с белым, синим и желто-зелёным проводами. Есть и китайцы с комбинациями серый + коричневый + белый, есть и сложные многожильные кабели, с которыми можно разобраться только по справочнику электрика.
В быту все эти кодировки взять неоткуда, поэтому будем ориентироваться на самую простую проводку.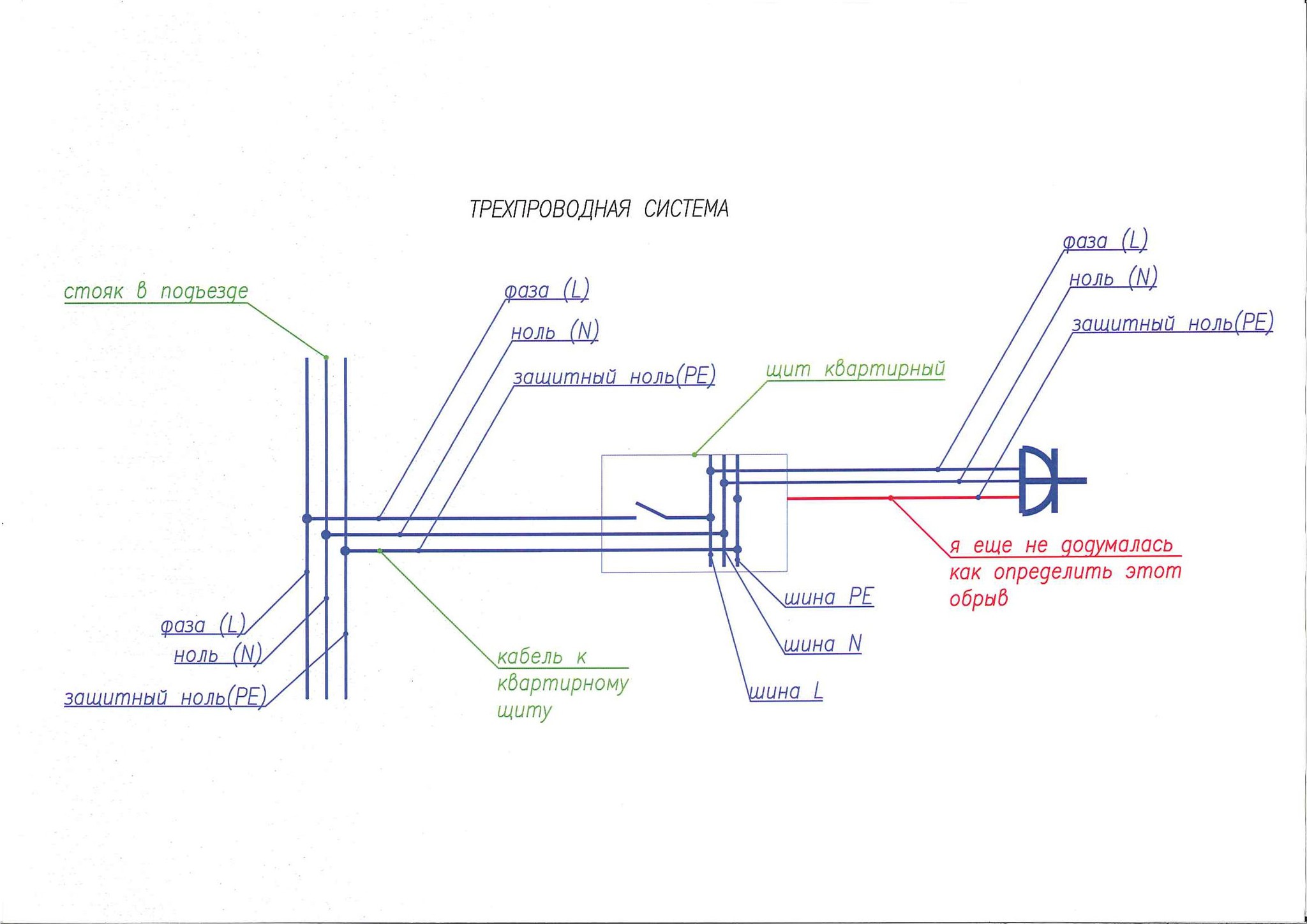 Простая — это кабель из трёх жил и бытовая задача, к примеру, установки розетки.
Простая — это кабель из трёх жил и бытовая задача, к примеру, установки розетки.
Стандартный бытовой провод с белым, синим и жёлто-зелёным цветом
Кодировка, маркировка и история
Идея разделить провода по цветам не нова — первые же эксперименты, как рисуют нам старые учебники, проводились с разноцветными клеммами и проводами. Всё та же незамутнённая простота осталась в автомобилях — синий и красный провод вряд ли перепутаешь. Правда, он иногда бывает чёрным, но это совсем другая история.
При изучении проводки самые важные для определения по цвету провода — не фаза, а земля и ноль, фазу всегда можно найти с помощью детекторной отвёртки или (практически) любого диода. А вот перепутать цвета земли и ноля иногда становится просто опасно, и определять, какого цвета провода фаза ноль земля надо заранее.
Цвет провода фазы
Как ранее было указано, особо фазу по цвету определять не требуется — почти всегда есть доступ к тому или иному инструменту для определения. Некоторый «зоопарк» в цветах наблюдается из-за того, что есть расширенные, не бытовые стандарты по цветовой дифференциации проводов, их используют настоящие электрики. Например, коричневый цвет говорит, что провод предназначен для розеток, а красный — для освещения. От этого зависит нагрузка и допустимые параметры работы.
Некоторый «зоопарк» в цветах наблюдается из-за того, что есть расширенные, не бытовые стандарты по цветовой дифференциации проводов, их используют настоящие электрики. Например, коричневый цвет говорит, что провод предназначен для розеток, а красный — для освещения. От этого зависит нагрузка и допустимые параметры работы.
Цвет провода земли
Заземление самый безальтернативный провод, у него всегда жёлто-зелёный цвет. Бывают отклонения, например, чисто жёлтый — когда провод импортный. В сети пишут, что встречается жёлто-зелёно-синий цвет провода, которым обозначают совмещённый рабочий нуль и землю.
Цвет провода ноля
У минуса небольшой выбор цветов — обычно это синий провод, который есть практически в любом кабеле, либо (очень редко) красный/вишнёвый. Как было сказано о земле — путать эти провода строго не рекомендуется.
Заключение
Фиксируем общую цветовую схему:
- Земля — цвет провода жёлто-зелёный или жёлтый цвет провода;
- Ноль — синий цвет;
- Фаза — цвет провода белый, красный, коричневый и любые другие незнакомые.

Цветовая маркировка проводов и шин
Здравствуйте, уважаемые читатели и гости сайта «Заметки электрика».
При проведении электромонтажных работ, очень часто поднимается вопрос о цветовой маркировки проводов.
Это раньше, так сказать в «застойное» время, применялись провода только белого цвета, реже черного.
Поэтому определить в электрической сборке фазу или ноль, занимало достаточно много времени. Приходилось прибегать к помощи указателей напряжения и различных аналоговых и цифровых приборов.
Чтобы этого избежать, нужно приводить цветовую маркировку проводов и шин к единому стандарту.
И как всегда обратимся к нормативным документам, а именно к ПУЭ, Глава 1, п.1.1.29. и п.1.1.30. Там четко сказано, что идентификацию жил проводов и шин по цветам или цифровым обозначениям необходимо использовать, согласно ГОСТ Р 50462-92.
И что же сказано в этом ГОСТе?!
Согласно ГОСТ Р 50462-92, п. 3.1.1, для идентификации проводников и шин могут быть применены следующие цвета: черный, коричневый, красный, оранжевый, желтый, зеленый, синий, голубой, серый, белый, розовый, бирюзовый.
3.1.1, для идентификации проводников и шин могут быть применены следующие цвета: черный, коричневый, красный, оранжевый, желтый, зеленый, синий, голубой, серый, белый, розовый, бирюзовый.
Согласно ПУЭ, п.1.1.29:
- нулевые рабочие проводники (N) должны иметь голубой цвет
- cовмещенные нулевые рабочие и нулевые защитные проводники (PEN) должны иметь голубой цвет по всей длине и желто-зеленые полосы на концах
- нулевые защитные проводники (РЕ) и проводники защитного заземления должны иметь желто-зеленый цвет
Приведу для примера несколько фотографий. Все нулевые рабочие проводники (N) подключены к шине (N) и имеют голубой цвет. Все нулевые защитные проводники (РЕ) подключены к шину (РЕ) и имеют желто-зеленый цвет.
А все остальные цвета, кроме голубого (синего) и желто-зеленого могут быть использованы в качестве фазных проводников.
На фотографиях ниже видно, что фазные проводники имеют белый цвет.
Цветовая маркировка проводов и шин при переменном трехфазном токе
Согласно ПУЭ, п.1.1.30, при переменном трехфазном токе шины фазы А должны иметь желтый цвет, фазы В — зеленый цвет, фазы С — красный цвет. Запоминается легко и просто в виде сокращения «ЖЗК», т.е. желтый, зеленый, красный.
Для наглядности приведу несколько примеров.
Система сборных шин напряжением 10 (кВ).
Два измерительных трансформатора НОМ-10 (кВ).
Отходящий фидер распределительной подстанции напряжением 500 (В).
Отходящие фидера секции 400 (В).
Как видите, на приведенных примерах цветовая маркировка шин при переменном трехфазном токе полностью соблюдается.
Кстати, не обязательно, чтобы шины были полностью выкрашены в тот или иной цвет. Вполне достаточно делать цветовую маркировку (в виде краски, наклеек, термоусадочных трубок, бирок и т.п.) в местах присоединения шин к коммутационным аппаратам.
Цветовая маркировка проводов и шин при переменном однофазном токе
Согласно ПУЭ, п.1.1.30, при переменном однофазном токе шина фазы В, присоединенная к концу обмотки источника питания, должна иметь красный цвет, а шина фазы А, присоединенная к началу обмотки источника питания, должна иметь желтый цвет.
К сожалению, наглядных примеров таких электроустановок у меня нет. Может у кого имеются фотографии, то буду очень благодарен, если Вы поделитесь.
Кстати, если шины однофазного тока являются ответвлением от системы трехфазного тока, то они обозначаются, согласно требований цветовой маркировки трехфазной системы.
Цветовая маркировка проводов и шин при постоянном токе
Согласно ПУЭ, п.1.1.30, при постоянном токе положительная шина («плюс») должна иметь красный цвет, отрицательная шина («минус») — синий цвет и нулевая рабочая («М») — голубой цвет.
В качестве примера приведу щит постоянного тока (ЩПТ) =220 (В).
А это выводы непосредственно с аккумуляторной батареи.
Кстати, со свинцовой-кислотных батарей СК-5 мы плавно переходим на необслуживаемые батареи Varta.
Дополнение
С 01.01.2011 отменен, указанный в начале статьи ГОСТ Р 50462-92. Вместо него вступил в силу ГОСТ Р 50462-2009, в котором некоторые пункты противоречат предыдущему ГОСТу. Например, в п.5.2.3 говорится, что для фазных проводников предпочтительны следующие цвета:
- серый
- коричневый
- черный
Для наглядности выкладываю фотографию распределительного щитка одного из банков, на котором мы производили электромонтаж.
По моему мнению, ранее принятая маркировка «ЖЗК» является более наглядной.
В однофазной сети для фазного проводника предпочтительным цветом является коричневый. Соответственно, что если однофазная сеть является ответвлением от трехфазной, то цвет фазного проводника должен соответствовать цвету фазного проводника трехфазной сети.
Также был введен запрет на желтый и зеленый цвета, применяемые по отдельности (п.5.2.1). Они должны быть использованы только в комбинации желто-зеленого цвета для защитных проводников РЕ. В связи с этим и была изменена маркировка трехфазной сети «ЖЗК», т.к. желтый и зеленый цвета применялись в ней по отдельности.
Цифровая маркировка цепей постоянного тока тоже была изменена (п.5.2.4):
- коричневый цвет — положительный полюс (+)
- серый цвет — отрицательный полюс (-)
- синий цвет — средний проводник (М)
Внимание!!! Хочу Вас предупредить, что не нужно сейчас бежать и изменять существующую маркировку. Ведь когда вводились объекты, действовал еще старый ГОСТ Р 50462-92. А вот при вводе в эксплуатацию уже новых электроустановок ГОСТом 50462-2009 пренебрегать не следует.
Если по каким то причинам нет возможности выполнить маркировку проводов и шин по вышеперечисленным требованиям, то можно использовать любые цвета. Но необходимо на концы жил намотать изоленту, наклейки, одеть кембрики или термоусадочные трубки соответствующего цвета, например, вот так:
И уже по традиции, смотрите видео по материалам данной статьи:
P.S. Уважаемые коллеги, я прошу Вас при выполнении электромонтажных работ соблюдать требования по цветовой маркировке проводов и шин. Давайте уважать друг друга.
Если статья была Вам полезна, то поделитесь ей со своими друзьями:
Расцветки проводки в Америке, Западной Европе. Частный электрик москвич
Какие цветовые коды оболочки
проводов используются для
обозначения в западных странах
при монтаже электропроводки
Кабели, провода, вся электропроводка,
с помощью которой производится электромонтажные
работы в доме, квартире в
электрощите, при монтаже
электроаппаратов имеет цветовую
маркировку. Цветовая маркировка
электропроводки при
распределении переменного и
постоянного тока какой-либо
ветви цепи обязательно имеет
цветовую маркировку.
В некоторых странах все цвета
проводов указаны в
нормативно-правовых документах,
в некоторых странах есть лишь
некоторые рекомендации по цвету
проводов для электромонтажа.
Посмотрим, какие правила
цветовой маркировки проводки, то
есть цвета изоляции провода,
существуют на Западе.
В Европе большинство стран
придерживается правил МЭК,
Международной Электротехнической
комиссии. Мы будем рассматривать
те правила, которые используются
для расцветки электропроводки
переменного тока.
Рассмотрим новые и старые
цветовые коды. Старая кодировка
не полностью учитывала точное
обозначение фаз. Электромонтажные
работы сейчас выполняются с
учетом новых правил цветовой
кодировки, а это более понятно и
удобно при электромонтаже.
Кстати, в Европе провод
защитного заземления везде
обозначается как зеленый с желтой полосой.
Цветовые коды электропроводки
МЭК, применяемые в большинстве
стран Европы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так обозначаются цвета
электропроводки в Европе. Если
производится монтаж
электропроводки в доме с
трехфазным напряжением, то по
цвету провода можно понять какую
функцию выполняет провод, какая
это фаза или это ноль.
А вот в США цветовая маркировка
электропроводки отличается. Там
есть маркировка Национального
Электрического кода. Провод
заземления в Америке или медный
оголенный, без изоляции, или
зеленый, или зеленый с желтой
полосой. Цвета провода черный,
красный и синий используются для
электропроводки с трехфазным
переменным напряжением
120 вольт. Цветовой код
коричневый, оранжевый и желтый
используется для электропроводки
с более высоким переменным
напряжением.
Вот цветовые коды
электропроводки переменного
тока, используемые в США:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так что в Штатах ноль в розетке
– белый провод, что для нашей
российской электропроводки в
доме не характерно.
Если вам нужно сделать
качественный монтаж
электропроводки в доме или
квартире, звоните. Я делаем
надежную электропроводку.
Обозначение L и N в электрике — RozetkaOnline.COM
Каждый раз, пытаясь подключить люстру или бра, датчик освещенности или движения, варочную панель или вытяжной вентилятор, терморегулятор теплого пола или блок питания светодиодной ленты, а также любое другое электрооборудование, вы можете увидеть следующие маркировки возле клемм подключения – L и N.
Давайте разберемся, о чем говорят обозначения L и N в электрике.
Как вы, наверное, сами догадались это не просто произвольные символы, каждый из них несет конкретное значение и выполняет роль подсказки, для правильного подключения электроприбора к сети.
« L » — Эта маркировка пришла в электрику из английского языка, и образована она от первой буквы слова «Line» (линия) – общепринятого названия фазного провода. Также, если вам удобнее, можно ориентироваться на такие понятия английских слов как Lead (подводящий провод, жила) или Live (под напряжением).
Соответственно обозначением L маркируются зажимы и контактные соединения, предназначенные для подключения фазного провода. В трехфазной сети, буквенно-цифровая идентификация (маркировка) фазных проводников «L1», «L2» и «L3».
По современным стандартам (ГОСТ Р 50462-2009 (МЭК 60446:2007), действующим в России, цвета фазных проводов – коричневый или черный. Но зачастую, может встречаться белый, розовый, серый или провод любого другого цвета, кроме синего, бело-синего, голубого, бело-голубого или желто-зеленого.
«N» — маркировка, образованная от первой буквы слова Neutral (нейтральный) – общепринятое название нулевого рабочего проводника, в России называемого чаще просто нулевым проводником или коротко Ноль (Нуль). В связи с этим, удачно подходит английское слово Null (нулевой), можно ориентироваться на него.
Обозначением N в электрике маркируются зажимы и контактные соединения для подключения нулевого рабочего проводника/нулевого провода. При этом это правило действует как в однофазной, так и трехфазной сети.
Цвета провода, которыми маркируется нулевой провод (нуль, ноль, нулевой рабочий проводник) строго синий (голубой) или бело-синий (бело-голубой).
Если уж мы говорим об обозначениях L и N в электрике, нельзя не отметить еще вот такой знак — , который также, практически всегда можно увидеть совместно с этими двумя маркировками. Таким значком отмечены зажимы, клеммы или контактные соединения для подключения провода защитного заземления (PE – Protective Earthing), он же нулевой защитный проводник, заземление, земля.
Общепринятая цветовая маркировка нулевого защитного провода – желто-зеленый. Эти два цвета зарезервированы только для заземляющих проводов и не встречаются при обозначении фазных или нулевых.
К сожалению, нередко, электропроводка в наших квартирах и домах выполнена с несоблюдением всех строгих стандартов и правил цветовой и буквенно-цифровой маркировки для электрики. И знать предназначение маркировок L и N у электрооборудования, порой, недостаточно, для правильного подключения. Поэтому, обязательно прочитайте нашу статью «Как определить фазу, ноль и заземление самому, подручными средствами?», если у вас есть какие-то сомнения, этот материал будет как нельзя кстати.
Цветовые обозначения фазы L, нуля N и заземления
Любой электрический кабель для удобства монтажа изготавливается с разноцветной изоляцией на жилах. При монтаже стандартной электропроводки обычно используются трехжильные кабели (фаза, ноль, заземление).
Фаза («L», «Line»)
Основным проводом в кабеле всегда является фаза. Само по себе слово «фаза» означает «провод под напряжением», «активный провод» и «линия». Чаще всего он бывает строго определенных цветов. В распределительном щитке фазовый провод, перед тем как идти к потребителю, подключается через устройство защитного отключения (УЗО, предохранитель), в нем происходит коммутация фазы. Внимание! С голой фазой шутки плохи, по этому, чтобы не спутать фазу с чем-либо еще — запомните: контакты фазы всегда маркируются латинским символом «L», а провод фазы бывает красным, коричневым, белым или черным! Если же вы не уверены в этом или проводка устроена иначе, то приобретите отвертку с простым индикатором фазы. Прикоснувшись его жалом к голому проводнику, всегда можно узнать — фаза это или нет по характерному свечению индикатора. А лучше сразу обратитесь к квалифицированному специалисту.
Ноль («N», «Neutre», «Neutral», «Нейтраль» «Нуль»)
Вторым немаловажным проводом является ноль, известный в народе как «провод без тока», «пассивный провод» и «нейтраль». Он бывает только синим. В квартирных распределительных щитках его нужно подключать к нулевой шине, она помечена символом «N». К розетке провод нуля подключается к контактам, также обозначенным знаком «N».
Заземление («G», «T», «Terre» «Ground», «gnd» и «Земля»)
Изоляция заземляющего провода бывает только желтого цвета с зеленой полоской. В распределительном щитке он подключается к шине заземления, к дверце и корпусу щитка. В розетках заземление подключается к контактам, обозначенным латинским символом «G» или с знаком в виде перевернутой и коротко подчеркнутой буквой «Т». Обычно заземлительные контакты на виду и могут выступать из розеток, становясь доступными детям, что порой вызывает у многих родителей шок, тем не менее эти контакты не опасны, хотя совать пальцы туда все же не рекомендуется.
Внимание! При работе с электрическими сетями под напряжением всегда велика вероятность поражения человека электрическим током или пожара. Если даже установлено УЗО, настоятельно рекомендуется соблюдать все меры предосторожности! Известно, что специальная конструкция такого выключателя сверяет синхронность работы фазы и нуля, и в случае, если УЗО обнаружит утечку тока фазы без возвращения каких-то его процентов по нулю, то немедленно разорвет контакт, что спасет человеку жизнь; однако если прикоснуться не только к фазе, но еще и к нулю — то УЗО не спасет. Прикосновение к обоим проводам смертельно опасно!!!
Расколотый | Красный против синего вики
Sideways — шестой эпизод Red vs. Blue: Zero . Премьера состоялась 14 декабря 2020 года для участников Rooster Teeth FIRST и 21 декабря 2020 года для широкой публики. Это 357-й канонический эпизод в целом.
Shatter Squad [править | править источник]
Viper [править | править источник]
Альянс Защиты [править | править источник]
Другое [править | править источник]
- Такер
- Несколько врачей (Только голос)
В воспоминаниях мы слышим, как несколько врачей объясняют Уэсту опасную процедуру, которую они проведут на очень молодом Востоке, которого боятся.Уэст говорит им сделать это, просто желая, чтобы его дочь выжила. Мы также слышим голоса Акселя и Зеро, которые обеспокоенно протестуют против действий Запада. По мере того как Восток становится все более напуганным, Уэст говорит ей не сопротивляться, пока врачи начинают операцию.
В наши дни мы слышим, как врачи пытаются реанимировать Такера, когда он падает. Они успешны, поскольку Такер просыпается в больничной палате в сопровождении своих старых друзей Вашингтона и Каролины. Рад видеть, что с ним все в порядке, Уош говорит Такеру, что он мог бы умереть, если бы врачи не вылечили его вовремя с помощью своих технологий.Такер, однако, очень расстраивается из-за потери своего меча, заявляя, что теперь он «наполовину человек». Уош смеется, пропустив выходки Такера.
В другом месте базы Раймонду не удается отремонтировать оборудование и хандры, он все еще опечален потерей Востока. Когда Один пытается его успокоить, Рэй объясняет, что он знал о состоянии Ист, когда он впервые увидел ее мерцание, обнаружив это в старых файлах GLASS. Она — «Холо-Эхо» — твердый клон, сделанный из фрагмента личности.Когда Один призывает Рэя перестать хандрить, входит Аксель и просит двоих пойти с ним.
Аксель, Раймонд, Уан и Каролина слушают разъяренный Запад, взбесившийся за комнатой, выражающий свою вину за провал Востока / Фазы. Остальные объясняют ему, что они хотят помочь Востоку, и умоляют его выйти и поговорить с ними. В конце концов, Уэст сталкивается с ними и объясняет, что он сделал с Востоком, когда она была молода. По словам Уэста, все началось с GLASS, специальной программы операций, подобной Project Freelancer, разработанной для победы в Великой войне с помощью шпионажа и науки.Программа запустила первый Shatter Squad и попыталась заполучить второй с Zero, в то время под кодовым названием «One», в качестве его лидера. К сожалению, программа не смогла и была закрыта после окончания войны. Чувствуя себя преданным, Зеро хотел доказать, что он могущественен, и зачислил Фэйза в свой синдикат. Затем Уэст показывает, что Восток чуть не умерла от обострения болезни, когда она была маленькой девочкой. Он обратился за помощью к Starlight Laboratories, чтобы спасти ее, что они и сделали с помощью экспериментов с инопланетянами.Аксель добавляет, что Ист сбежал несколько лет назад и в конце концов присоединился к Viper.
В последнем храме, Гадюка стоит у входа. Zero и Phase, которые теперь контролируют меч Такера, используют свои ключи, чтобы успешно получить доступ. Вернувшись на базу, Крошка доставляет сообщение от Зеро в Shatter Squad. В сообщении Зеро насмехается над командой, заявляя, что он открыл последний храм и отправляет им свои координаты. Один бросается в бой, но остальные остаются на месте, неуверенные в своих способностях остановить Вайпера.Один напоминает им, что Зеро — всего лишь один человек, и призывает их в своей речи продолжать борьбу за спасение Востока. Воодушевленные и решительные, Shatter Squad модернизируют свое оружие и броню и уходят, чтобы остановить Вайпера.
Скоро в продаже
- Настоящее имя Уэста — Брюс.
- Это единственный эпизод в сезоне, в котором нет боевых сцен.
- В The Chorus Trilogy было показано, что убийство владельца меча было единственным способом получить контроль над мечом.Учитывая, что Такер пережил нападение, вполне вероятно, что какое-то время он был клинически мертв.
What Red Vs. Синий: приближаются к нулю (и что изменилось)
Red vs. Blue: Zero — восемнадцатый и новейший сезон продолжительной серии, но с некоторыми изменениями. Вот в чем суть нового сезона.
Красный против синего: ноль — новейший и восемнадцатый сезон давней веб-серии , вдохновленной Halo- от Rooster Teeth.Хотя первая серия уже выпущена, новый сезон официально начинается 9 ноября 2020 года. С некоторыми изменениями стиля и тона даже некоторые давние фанаты могут задаться вопросом, о чем новый сезон. Вот все, что вам нужно знать.
С последним сезоном Red vs.Blue, — это еще один шаг вперед по сравнению с окружением Halo и материалами, которые вдохновили его. На этот раз локации и ресурсы Halo , отличные от , повсюду. К старым активам добавляются не только новые скины. Показаны новые монстры и даже оружие, которых никогда не было в игре Halo . Хотя можно с уверенностью предположить, что это, вероятно, не дразнилки нового оружия или монстров из проблемного Halo: Infinite , поскольку они были взяты из множества отмененных видеоигр, все же приятно видеть проблески новых мест, врагов и предметов. .
Продолжайте прокручивать, чтобы продолжить чтение
Нажмите кнопку ниже, чтобы начать эту статью в режиме быстрого просмотра.
Связано: сколько скинов Halo Combat Evolved будет стоить на модели Infinite
Основная цель игры Red vs.Синий: Zero находится между разношерстной командой Shatter Squad и таинственным новым отрядом, возглавляемым лидером по имени Зеро. Загадочный Зеро хочет получить Абсолютную Силу (что бы это ни было), и Shatter Squad должен объединиться, чтобы остановить Зеро и спасти галактику. Это знакомая предпосылка, но в основном она работает, особенно потому, что члены Shatter Squad — свежие и интересные персонажи, которые пытаются понравиться как давним фанатам Red vs. Blu e, так и новичкам в серии.
Чем отличается красный vs.Синий: Zero
Хотя новое телешоу Halo предположительно находится в разработке на Showtime, Red vs. Blue отмечает свой восемнадцатый сезон с некоторыми существенными изменениями.Хотя в Red vs. Blue: Zero есть знакомые персонажи, большая часть актерского состава совершенно новые. Shatter Squad возглавляет Агент Один и состоит из новобранцев Акселя, Востока, Раймонда и Уэста. И наоборот, команда Зеро состоит из сильного Дизеля и быстрой Фазы, способной телепортироваться. Эти новые персонажи привносят некоторую свежесть в серию, но они также заставляют ощущать Red vs. Blue: Zero совсем по-другому.
Есть еще шутки, но все это отходит на второй план к действию и долгим боевым сценам.Это далеко от глупых выходок, замеченных в предыдущих сезонах шоу, и тон ощущается как немного более взрослая версия Звездных войн: Войны клонов с точки зрения тона и действия. Это рассказ о хорошем и плохом на фоне Halo , который больше не похож на Halo . Помимо доспехов и транспортных средств, которые можно было увидеть в играх Halo , игра Red vs. Blue: Zero проходит мимо своего первоначального вдохновения и попадает на, казалось бы, новую территорию.
В центральной истории достаточно загадок, чтобы зрители возвращались к ней снова и снова. В то время как старый Red vs. Blue больше всего привлекал комедию и анекдоты, Red vs. Blue: Zero больше посвящен действиям и повествованию.Даже с этими изменениями поклонники Halo должны по-прежнему наслаждаться шоу, поскольку недавно сформированный Shatter Squad сражается с Зеро, чтобы спасти галактику.
Далее: Как Halo Infinite может вернуть Halo к успеху
Обзор Razer Kaira : отличный помощник для Xbox
Об авторе
Остин Кинг
(Опубликовано 1017 статей)
Остин Кинг — автор нескольких книг и ведущий подкастов Dragon Quest FM и JRPGs & Me.Вы можете найти его в Twitter @DragonQuaustin.
Ещё от Austin King
Обзор
: красный против синего: ноль «столкновения»
ОБЗОР (СПОЙЛЕРЫ)
Shatter Squad вступает в бой с Viper в городе, но проигрывает на каждом шагу. Фейс и Дизель уходят, а Зеро сковывает Акселя с помощью своего меча, прежде чем нанести сокрушительный удар остальной части отряда, в том числе нокаутировать Уэста.Все болят, когда возвращаются на базу, в том числе и включают Акселя из-за того, что он каким-то образом явно знаком с Зеро. Но когда Один рассказывает Каролине о Зеро, упомянув, что ему нужен только еще один ключ, она решает не подчиняться приказам и искать Такера, у которого может быть ключ, который хочет Зеро.
НАШЕ ПРИНЯТИЕ
Shatter Squad и Viper наконец-то сошлись, когда мы подошли к середине сезона, показывая, как далеко должен зайти новый состав, чтобы победить своих противников, включая понимание трещин в их командной работе.Понятно, что многим из членов Shatter Squad нужно преодолеть некоторые из своих проблем, но проблема заключается в том, что неясно, что именно выходит за рамки общего ворчания, исходящего от Единого и Востока. У Востока есть проблемы с отцом Уэстом, у Акселя есть некоторая смутная связь с Зеро, заставляющая окружающих сомневаться в его лояльности (несмотря на то, что у них не было возможности увидеть, как он колеблется, что неясно, даже если он и делал, поэтому «Я доверял «ты» выглядит чересчур наверху), а Один хочет… чего-то? Некоторые отмечают, что на данный момент она кажется немного повторяющимся персонажем по сравнению с Востоком, у которого, по крайней мере, есть заметная причина для ее отношения, которое имеет потенциал для роста и развития, а именно ее сложные чувства к Западу.У одной, с другой стороны, есть предыстория ваших мертвых родителей, и она хочет проявить себя, но на этом сейчас все. Ах да, а Раймонд и Тайни истощают мою жизнь всякий раз, когда они на экране.
Затем у нас есть Viper, которые зарабатывают себе репутацию настоящих угроз с помощью своего рода плана и достаточно отличны по характеру и дизайну, так что вы можете сказать, о чем каждый из них. Дизель — сумасшедший берсерк (которого давно переделали, поэтому я не могу использовать ни одну из моих шуток «Агент Андерсмит сошел с ума»), Фаза — одна со странными способностями, у которой есть личная неприязнь (напомните вам о всех, кто носит розовое в этом сезоне?), а Зеро — вдохновитель, который хочет изменить мир по своему образу.За исключением того, что чем больше я слышу Zero talk и чем больше мы узнаем о нем, тем больше вопросов это вызывает, и не в хорошем смысле. В прошлый раз он произнес фразу о «Я не простой смертный, я призрак», он сказал Акселю, что существуют «настоящие монстры», но мы не получили более подробной информации об этом, и теперь он звонит. Одна из низших версий самого себя, которую он называет ее «тенью». Все они сами по себе кажутся аккуратными, но на самом деле они ничего не говорят… прямо сейчас. И их нужно начинать в ближайшее время.Больше всего мы можем почерпнуть из этого то, что Один имеет с ним больше связи, чем просто их числовые имена, которые уже подразумевали связь, но в этих последних четырех эпизодах, похоже, у них нет НИЧЕГО общего, кроме этого.
Еще одна вещь, о которой я хочу поговорить на этой неделе, — это мои смешанные чувства по поводу выбора режиссера, который мы видели до сих пор. Одно из того, что я не совсем замечал до сих пор, — это использование камеры, при которой она иногда перемещается, как будто снимает реалити-шоу, что может быть для добавления некоторого чувства реализма, но обычно служит только для создания моментов, которые должны были быть серьезными. в меньшей степени.Хотя более заметный ход был на этой неделе, который решил разделить борьбу на Франкенштейна, прыгая между неупорядоченными клипами, что в конечном итоге сбило меня с толку, когда что-то происходило. У меня есть мысли о возможном возвращении Такера, но я оставлю это на следующий раз. Главное, что я хочу сказать, это то, что кажется, что эта новая команда очень весело играет с разными стилями и техниками, чтобы сделать этот сезон отчетливо своим, и я восхищаюсь и уважаю это, я просто надеюсь, что это приведет к чему-то, что заставит использовать все того стоит.
Нравится:
Нравится Загрузка …
Банк Блю Хиллс — Проект нулевой фазы
Дом
О
Работа
Insights
Новости
Карьера
Контакт
Назад
Академический
Гостеприимство
Здравоохранение
Жилой
Розничная торговля
Рабочее место
На досках
Концептуальный дизайн
ГлавнаяО компании
Работа
Академический
Гостеприимство
Здравоохранение
Жилой
Розничная торговля
Рабочее место
На досках
Концептуальный дизайн
АналитикаНовостиКарьера
Контакт
1
2
Предыдущий
Следующий
Часы
КарьераО насКонтактОфисные ресурсы
Шоураннер
Zero Торриан Кроуфорд и звезда Фиона Нова, интервью
За 17 лет с момента своего дебюта классический научно-фантастический веб-сериал Red vs.Blue находится в состоянии почти постоянной эволюции. Его стиль анимации и повествования стал более сложным, его повествовательные амбиции увеличились, а стоящая за ним студия — Rooster Teeth из Остина — превратилась в электростанцию с охватом, выходящим далеко за рамки того, что начиналось как глупая серия короткометражек о некоторых из них. Halo персонажей. В некотором смысле постоянный рост и изменения за Red vs. Blue — это такая же часть его успеха, как и его неизменная приверженность комедийному научно-фантастическому тону, который повлиял на самые ранние эпизоды.Если вы хотите играть в этой узнаваемой забавной песочнице, вы можете разделить серию на множество различных направлений, что имел в виду сценарист и режиссер Торриан Кроуфорд, когда предлагал Red vs. Blue: Zero , следующий этап одного из любимых интернет-шоу. Премьера нового сериала состоится 9 ноября.
.
«Изначально меня вдохновили некоторые из предыдущих сезонов, которые больше фокусировались на действии или включали больше элементов действия, я думаю, в 8, 9 и 10 сезонах, когда в них участвовал класс персонажей под названием« Фрилансеры »[ The Project Freelancer Saga ], когда они включали легендарного режиссера анимации Монти Оума », — сказал Кроуфорд SYFY WIRE.«Меня действительно вдохновила последовательность событий, которые произошли в лоре RvB . Так что я действительно просто хотел развить это. Когда я пошел и обратился к [сценаристу, режиссеру, продюсеру и актеру RvB ] Мэтту Внутри Hullum мы как бы назвали это « RvB встречает Fast & Furious », что является действительно интересным способом сказать: «Эй, мы хотим сделать RvB , но мы хотим сделать это так». Приключение, этот стиль боевого ограбления, немного смешанный с обычными, хорошо написанными комедийными корнями, которые так глубоко укоренились в сериале.'»
В то время как комедийные корни Red vs. Blue хорошо представлены в Zero , сериал в его окончательной форме также является динамичным и ярким отражением желания Кроуфорда — в его первый раз в качестве шоураннера Rooster Teeth после шести лет работы в компании над такими шоу, как Death Battle! и gen: LOCK — чтобы добавить во франшизу больше удовольствия от боевиков. Хотя он по-прежнему выглядит и ощущается как Red vs. Blue , Zero заимствует большую часть своей чванливости и философии действия из любимых боевиков Кроуфорда и принимает форму классической истории «Команда собирается вместе, чтобы выполнить работу». как группа воинов с различными навыками и часто сталкивающимися личностями, должны объединиться, чтобы сразиться с главным злодеем, Зеро, который находится в разгаре безжалостных поисков «Абсолютной силы».«
«Я действительно хотел исследовать стили боевиков из фильмов, которые я смотрю, например, The Raid , где происходят эти сумасшедшие, высоко поставленные, энергичные бои, но в тесном коридоре, и вы сражаетесь с целой массой парней. Или другие фильмы, такие как Flash Point с Донни Йеном и Ip Man , а затем эти более масштабные приключенческие боевики, которые действительно очень забавны », — сказал Кроуфорд. «Я думаю, что когда вы думаете о таких фильмах, как Fast & Furious , это одна из тех вещей, где вы не можете не принять то, что в них происходит, потому что вы знаете, что это смешно.Вы знаете, что это тропия; ты знаешь, что это дрянно. Именно так я разработал в этом сезоне RvB . И, честно говоря, я думаю, что RvB — идеальное судно для этого, потому что, на мой взгляд, это может быть что угодно. Они так много сделали с шоу. У них были некоторые из тех ранних битов действий. Само шоу укоренилось в комедии, но на протяжении всего сериала они исследуют более глубокие характеристики. Итак, когда дело доходит до этого сезона, я как бы намеренно построил тропический сезон с конкретной целью — просто развлечься, то, что вы можете просто наблюдать.Это просто должно быть весело. На самом деле это не значит, что нужно слишком много думать. В этом сезоне очень хорошо известно, насколько оно дрянное ».
Несмотря на то, что игра Red vs. Blue: Zero радостно играет с образцами боевиков, она также должна создать привлекательный новый состав персонажей, которые помогают продвигать эту философию приключенческого боевика. Это означало создание ансамбля, составляющего основу шоу, команды, известной как «Shatter Squad», и выбор подходящего человека на главную роль Агента Один, таинственного бойца, которому есть что доказать.Для этого Кроуфорд обратился к Фионе Нове, начинающей актрисе озвучивания, которая наиболее известна своей работой на игровом канале Rooster Teeth Achievement Hunter .
«Торриан конкретно указал, что он хотел, с точки зрения того, кто будет озвучивать его главного персонажа, первого агента, — говорит Нова. «Я впервые выступаю в роли ЗК, так что было немного нервно иметь такую сильную позицию и думать:« Смогу ли я отдать должное его персонажу? » Он очень верил в меня и верил в меня, и он очень помогал мне во всем.Я имею в виду, что все в команде всегда помогали мне и давали мне много советов и уловок, и я думаю, что к концу этого я действительно нашел голос первого агента. Я вижу прогресс от первого эпизода к последнему, насколько я слышал ее голос. Так что да, это точно было очень захватывающе ».
Создавая характер Агента Один и четкую дугу, которую она демонстрирует в течение Ноль , Кроуфорд хотел большего, чем актер, который бы поставил строки.Помимо того, что он уделял первоочередное внимание выбору чернокожей женщины на эту роль, ему также был нужен творческий партнер, кто-то, кто будет информировать персонажа, когда она оживает. Похоже, он обнаружил это в «Нове», и, поскольку они оба приступили к новым ролям в своей работе над сериалом, сформировалось родство.
«Тот факт, что Фиона никогда не делала этого раньше, на самом деле был очень хорош, потому что у меня было представление о том, кто такой Агент Один, но это то, что я действительно хотел создать персонажа и построить ее вместе с Фиона, — говорит он.«Я думаю, что если вы действительно посмотрите на это с производственной точки зрения, то на самом деле это и наш первый раз, когда я режиссирую голосового актера, а Фиона занимается озвучкой. Это оба наши первые разы, и я действительно очень хотел, чтобы это путешествие и эти конкретные знания помогли нам на самом деле помогли нам развить персонажа, потому что она новый персонаж. Итак, я хотел, чтобы мы оба, а также другие сценаристы, которые у меня есть, и другие люди, которые работают в команде, по-настоящему прочувствовали этот персонаж и заставили ее расцвести. ее собственная личность, вроде того, как мы находимся и находимся на наших первых позициях в сериале с самого начала.«
Создание голосового состава команды мечты, в который также входят таланты Ноэля Уиггинса, Дженнифер Тидуэлл, Джеб Агилар-Кендрик, Андре Уэллетт и других, было приоритетом для ансамблевой динамики Shatter Squad в Red vs. Blue: Zero , но чувство совместного родства распространилось далеко не только на актерский состав, но и на команду аниматоров. В стремлении создать динамичные, изобретательные боевые сцены, которые также смогли передать характер и историю, Кроуфорд искал лучших аниматоров, которых он мог найти, и приложил все усилия, чтобы сериал так же отражал их видение, как и его собственное.
«Итак, в основном, я и художники по раскадровке рассказываем о моих идеях, а мой режиссерский стиль в большей степени выражается так:« Я хочу знать, о чем вы думаете, творчески. Я хочу знать, что вы чувствуете. Я хочу поговорить с вами. об этих вещах. Я хочу разбираться в боевых действиях »и тому подобном. Они берут ту энергию и идеи, которые у меня есть, и они используют их и создают раскадровки. А затем раскадровки попадают к аниматорам, и это вроде того То же самое и с аниматорами.Мы выбрали нескольких лучших аниматоров — Мэтта Друри, Джо Вик, Питера Дэнга и Чарльза Джонсона — и они потрясающие.И это вроде как: «Эй, вот доски. Это вдохновение. У меня есть идея, стиль, которого я хочу достичь. Вы берете всю эту информацию и бежите с ней ». Многие действия, которые вы видите, я анимировал сам, но то, что я не оживлял, — это потому, что эти аниматоры пошли, и они действительно выложились на полную, и они вложили в это свое сердце, и они очень увлечены вышло офигенно. Вот как я подхожу к действию. Мы придумываем правила, стиль, а потом аниматоры вроде идут .Я не слишком разборчив и не люблю давать обзоры, и не слишком огорчаюсь, потому что мне нужен их творческий подход. Я хочу, чтобы они верили в себя, и я хочу, чтобы они выражали себя ».
Этот дух коллективного творчества пронизывает серию Red vs. Blue: Zero , шоу, которое в превью эпизодов SYFY WIRE удалось увидеть перед премьерой. — полет и опасность того, что вас вырвет в шлеме.Это смесь всего, что было в Red vs. Blue раньше, и некоторых вещей, которых не было. Кроуфорд и Нова вошли в историю Rooster Teeth, став первым черным шоураннером и черным ведущим актером, соответственно, почти за два десятилетия Red vs. Blue , и для них эта инклюзивность была перенесена на всю серию, а не только на с точки зрения людей, которые его создали, но с точки зрения его способности охватить другую аудиторию.
«Думаю, я бы сказал, что одна большая вещь, которая меня радует в этом сезоне, — это то, насколько разнообразен актерский состав, а также то, что за кадром.Это истории, написанные множеством разных людей, и я думаю, что это превратилось во что-то действительно удивительное », — говорит Нова.« Я очень рада, что эта история будет рассказана, тем более, что так много замечательных людей работали. в теме. Я не смотрел много Red vs. Blue в прошлом, но я считаю это идеальным входом для таких же людей, как я, которые видели это шоу, кому интересно, кто видел, как это наследие прошло, и они могут быть напуганы, увидев, что существует 17 сезонов.И они видят эту возможность, чтобы сказать: «О, мы можем начать все заново. Я собираюсь начать прямо здесь. Я думаю, что это действительно крутая часть, и я думаю, что это большая эволюция и определенно следующий шаг к тому, что будет с Red vs. Blue ».
Red vs. Blue: Zero премьера 9 ноября на Rooster Teeth для подписчиков Rooster Teeth FIRST. Новые эпизоды будут приходить еженедельно, и каждый эпизод можно будет бесплатно смотреть на Rooster Teeth через неделю после его ПЕРВОЙ премьеры.
Синхронизация с нулевой задержкой, несмотря на неоднородности в релейной системе
Abstract
Новым предложением для синхронизации запаздывающих связанных нейронов без запаздывания является их косвенное соединение через третий ретрансляционный нейрон. В этом исследовании мы разрабатываем карту Пуанкаре, чтобы исследовать устойчивость синхронности в такой релейной системе к неоднородности нейронов и синаптических параметров. Мы показываем, что, когда неоднородность не нарушает симметрию системы, синхронность сохраняется, а в некоторых случаях неоднородность усиливает синхронность.С другой стороны, если неоднородность нарушает симметрию системы, синхронизация с нулевым запаздыванием не может быть сохранена. В этом случае мы даем аналитические результаты для фазовой задержки импульса нейронов в стабильном состоянии.
Образец цитирования: Гасеми Исфахани З., Вализаде А. (2014) Синхронизация без запаздывания, несмотря на неоднородности в релейной системе. PLoS ONE 9 (12):
e112688.
https://doi.org/10.1371/journal.pone.0112688
Редактор: Матяз Перк, Университет Марибора, Словения
Поступила: 29 июля 2014 г .; Принята к печати: 10 октября 2014 г .; Опубликован: 8 декабря 2014 г.
Авторские права: © 2014 Гасеми Исфахани, Вализаде.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Авторы подтверждают, что все данные, лежащие в основе выводов, полностью доступны без ограничений. Все соответствующие данные находятся в документе и его файлах с вспомогательной информацией.
Финансирование: У авторов нет поддержки или финансирования, чтобы сообщить.
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
По всей коре пиковая активность групп клеток демонстрирует различные паттерны синхронности как во время спонтанной активности, так и при сенсорной стимуляции [1] — [7]. Синхронному возбуждению нейронов уделяется много внимания в связи с генерацией ритмов мозга и обработкой информации в различных аспектах нейронных систем, таких как избирательное внимание и проблема связывания [8] — [12].Синхронизированные сети оказывают более сильное влияние на свои целевые сети, и вовлечение целевой сети устанавливает исключительную нейронную связь [13]. Была выдвинута гипотеза, что динамически изменяющийся паттерн когерентной активности может перемещаться поверх анатомической структуры, обеспечивая гибкие нейронные коммуникационные пути [14] — [16].
Генерация синхронизации сетями взаимосвязанных нейронов является предметом многих теоретических и численных исследований [13], [17] — [24]. Механизм этих явлений был предметом противоречивых дебатов в более общем контексте; Помимо своей функциональной значимости, синхронизация с нулевым запаздыванием среди таких удаленных нейронных ансамблей должна быть установлена с помощью механизмов, которые способны компенсировать задержки, вовлеченные в нейронную коммуникацию [25] — [27].
Пара нейронов может синхронизироваться либо через прямое соединение, либо в результате общих входных сигналов, и вполне вероятно, что за синхронизацию на разных уровнях отвечают различные механизмы (различая, например, локальную и удаленную синхронизацию) и разные мозговые структуры. Ранние исследования синхронизации нейронов с отложенными связями показали, что возбуждающие связи не всегда синхронизируют нейроны, и фактически они обычно приводят к противофазной активации [28] — [30].Позже была разработана почти полная структура, раскрывающая роль кривой фазового ответа (PRC) в синхронизации нейронов с отсроченным сцеплением [31] — [33]. PRC отслеживает, насколько входной сигнал опережает или задерживает следующий всплеск в колебательном нейроне в зависимости от того, где в цикле применяется вход [34] — [36], и определяется типом бифуркации, которая приводит к повторному срабатыванию импульса. нейрон [34], [35], [37], но см. [38].
На синхронизацию также влияет конфигурация взаимодействия нейронов.Fischer et al. [39] представили новый механизм синхронизации через динамическую ретрансляцию, а затем последовали несколько других исследований [40] — [42]. Было показано, что две отдаленные популяции нейронов способны синхронизироваться с нулевым запаздыванием по времени, если третий элемент действует как реле между ними. Этот механизм оказался чрезвычайно устойчивым для широкого диапазона задержек проводимости и типов клеток [43]. Биологическая актуальность концепции обоснована предложением таламуса и гиппокампа в качестве стержневых регионов, генерирующих изохронную синхронизацию между удаленными корковыми областями посредством механизма динамической ретрансляции [44].Интересно, что исследования связности в коре головного мозга приматов идентифицировали ретрансляционный паттерн как наиболее часто повторяющийся мотив на уровне кортикокортикальных связей в зрительной коре, сигнализируя о функциональной значимости этой топологии в корковых сетях [45] — [49]. Синхронность, вызванная конфигурацией реле, основана на симметричном перераспределении входящих сигналов реле между двумя внешними нейронами [50]. Эта симметрия требует как одинаковых параметров внешних нейронов, так и симметричных связей.В минимальной модели нейроны характеризуются частотой их активации, а связи — синаптической силой и временем задержки. Все эти параметры имеют существенную неоднородность в мозговых сетях [36], [51] — [53], и вполне разумно исследовать, как такие неоднородности могут влиять на свойства синхронности релейной системы. В этом исследовании мы подробно исследуем роль неоднородности в параметрах нейронов и связей на синхронизацию внешних нейронов в релейной системе.Мы используем приближение редукции фазы и карты Пуанкаре для получения аналитических результатов об устойчивости синфазных (или почти синфазных) решений при наличии неоднородности. Исследуется роль скорости возбуждения нейронов, силы синапсов и времени задержки передачи. В качестве основного результата исследования мы показываем, что симметричные неоднородности (те, которые сохраняют симметрию) оказывают незначительное разрушающее влияние на синхронность, а в некоторых случаях они могут даже улучшить ее. С другой стороны, мы показываем, что релейная система уязвима для неоднородностей, которые нарушают симметрию системы.Аналитические результаты подтверждаются численными экспериментами на нейронных моделях на основе проводимости.
Методы
В нашем моделировании мы используем модель Ходжкина-Хаксли (HH), описываемую набором из четырех переменных, где — мембранный потенциал, а также переменные активации и инактивации натриевого тока и переменные активации калиевого тока. Соответствующие уравнения движения: (1) где — внешний ток. Параметры и являются соответствующими реверсивными потенциалами и представляют собой емкость на единицу поверхности.Мы используем следующие типовые значения параметров: и. Функции и и характерные времена (в миллисекундах) задаются: с и. Напомним, что при малых значениях система достигает устойчивой неподвижной точки (при). Переход от режима покоя к пиковому режиму опосредуется докритической бифуркацией Хопфа при критическом значении входного тока. Синаптический ток моделируется формулой (2), где функция (3) показывает временной ход постсинаптической проводимости после каждого импульса пресинаптического нейрона в определенный момент времени.Временная задержка — это время, необходимое для передачи сигнала от пре- к постсинаптическому нейрону, в данном случае от -го нейрона к-му. Реверсивный потенциал синапса составляет и определяют время нарастания и время затухания синаптического ответа соответственно. Устанавливаем моделировать возбуждающие синапсы, и.
Модели с пониженной фазой
Переход от покоя к повторяющейся активации для нейрона HH опосредуется субкритической бифуркацией Хопфа [54]. При надпороговом постоянном токе модель HH имеет стабильный предел, динамика которого вокруг предельного цикла может быть хорошо аппроксимирована методом уменьшения фазы [54].
Предполагая, что сеть связанных осцилляторов предельного цикла описывается формулой (4) где — состояние th осциллятора, F (X) — базовое векторное поле, которое описывает динамику одиночного осциллятора. A — это матрица смежности сети, а V определяет функцию связи. Мы предполагаем, что изолированный нейронный осциллятор имеет устойчивый предельный цикл с периодом, тогда скалярная фазовая переменная может быть определена для всех X в некоторой окрестности притягивающего предельного цикла, эволюция которого выводится из цепного правила (5)
Используя фазовую чувствительность каждого осциллятора и отбрасывая член ошибки, динамика системы может быть сведена к фазовому уравнению (6), которое справедливо в притягивающей окрестности предельного цикла.В предположении, что компоненты имеют ненулевые значения только в направлении напряжения, мы можем определить фазовую чувствительность каждого генератора как нормированную кривую фазовой характеристики (PRC) следующим образом [54].
Предположим, период колебаний. Краткий стимул применяется к переменной напряжения в разное время между двумя последовательными импульсами нейрона. Это приводит к изменению времени следующего всплеска. Для малых возмущений PRC определяется как (7)
Фазовая чувствительность — это PRC, деленная на амплитуду малого возмущения [55].Поскольку PRC и фазовая чувствительность линейно зависят в малом пределе, мы использовали их одинаково, когда предполагалась их функциональная форма. В наших аналитических исследованиях импульсные нейроны аппроксимируются фазовыми осцилляторами, а синаптические токи — импульсными стимулами. Затем модель сводится к (8) где — время спайка осциллятора, которым является пресинаптический нейрон, к осциллятору в качестве постсинаптического нейрона, а — сила связи между нейроном и.
Во всех симуляциях начальные значения для динамических переменных выбираются из равномерного распределения в соответствующем диапазоне для каждой переменной.Результаты записываются после отбрасывания 50 периодов, чтобы гарантировать, что на результаты не повлияет переходная динамика.
Результаты
Два взаимно связанных нейрона
В этом разделе мы разрабатываем карту для аналитического изучения состояния синхронизации двух нейронов, связанных взаимными импульсными связями с задержкой. Карта и формула, представленные здесь, дополняют недавнее исследование [56] и дают более точные результаты для более широкого диапазона параметров (см. Ниже).Чтобы построить карту, мы записываем фазу нейрона в момент импульса нейрона,. В установившемся режиме синхронизации 1∶1, в зависимости от фазового запаздывания импульсов двух нейронов и задержки, могут наблюдаться две разные ситуации (изображенные на рис. 1). В первом случае (случай 1) между каждыми двумя спайками двух нейронов оба нейрона или ни один из них получают синаптическую стимуляцию (рис. 1а). В другом случае (случай 2) между каждыми двумя спайками нейронов только один из нейронов испытывает случайную синаптическую стимуляцию (рис.1б). В обоих случаях мы имеем (см. Рис. 1): (9) где () — разность фаз двух нейронов во время пика первого (второго) нейрона и будет использоваться как фазовая задержка нейронов в заблокированных состояниях. Предполагая, что вычитание приведенных выше уравнений дает (10) где период (интервал между всплесками) в заблокированном состоянии, может быть получен из (11)
Заблокированное состояние характеризуется неподвижными точками уравнения. 10. Для случая 1 существует другое соотношение между разностями фаз (см. Рис.1а). Это основная поправка к модели, введенная в предыдущем исследовании, в котором предполагалось, что она верна (см. Уравнения 8–10 в [56]). Установка в уравнении. 10 и исключая период для случая 1, получаем (12)
Учитывая функциональную форму фазовой чувствительности, это неявное уравнение дает фазовую задержку в заблокированном состоянии как функцию параметров, и.
Для второго случая последовательность спайков нейронов и падающих синаптических импульсов аналогична изображенной на рис.1b. В этом случае неподвижные точки карты Ур. 10 можно найти из (13), где и которое можно вывести из рис. 1b.
Линеаризирующее уравнение. 10 вокруг неподвижных точек дает условие устойчивости решений (14), где штрих обозначает производную по.
Стоит отметить, что в симметричном однородном случае, когда, и, Ур. 10 сводится к двум решениям и. Синфазный (синхронный) режим является стабильным, если и условие устойчивости для противофазного зажигания есть.Обратите внимание, что система может показывать бистабильность, если и синфазные, и противофазные решения (локально) стабильны, но с каноническими формами PRC (и фазовой чувствительностью) для нейронов типа I () и типа II (), только одно из решений стабильны. Также для некоторых значений времени задержки все фазовые запаздывания являются фиксированными точками. Например, для канонических нейронов типа II это происходит для. В этом случае левая часть уравнения. 14 всегда равен нулю, и все фазовые запаздывания нейтрально стабильны. В этом случае начальные условия определяют фазовую задержку в заблокированном состоянии (рис.2а).
Рис. 2. Однородная и неоднородная система напрямую связанных нейронов.
(а) Синхронизированные состояния двух непосредственно связанных идентичных нейронов типа II. В зависимости от времени задержки синфазный или противофазный режимы стабильны с соответствующими отрицательными показателями Ляпунова, которые показаны для обоих состояний (левая панель). Разность фаз () срабатывания двух идентичных нейронов Ходжкина-Хаксли показана на правой панели. (б) Синхронизированные состояния двух непосредственно связанных нейронов при несовпадении частот.Численные решения (голубой) подтверждают достоверность аналитических результатов, полученных с помощью линейного приближения (темно-синий). Также показаны показатели Ляпунова для каждого из заблокированных состояний. Заштрихованная область показывает области, в которых режим синхронизации 1À1 не виден в численных результатах, а штриховые серые линии — граница устойчивости аналитического решения с отрицательными показателями Ляпунова. На правой панели показана разность фаз для двух нейронов HH с разными скоростями возбуждения.
https: // doi.org / 10.1371 / journal.pone.0112688.g002
Взаимосвязанные нейроны при наличии неоднородности
Несоответствие частот
Неоднородность может проявляться в системе из-за несоответствия в параметрах нейронов (а именно, их скорости активации в минимальной модели, которую мы использовали), и / или из-за разницы в параметрах связи, то есть задержках или синаптических силах. При наличии рассогласования собственных частот при симметричных связях, то есть, и, разность фаз двух нейронов в режиме фазовой синхронизации 1-1 может быть рассчитана по формуле.10. Возьмем разность фаз как, где — разность фаз однородной системы. Для небольшого рассогласования мы предполагаем, что отклонение от разности фаз однородной системы,, также мало, и его динамика может быть описана линеаризацией уравнения. 12 или уравнение. 13.
В качестве примера рассмотрим канонические нейроны II типа с. Эта модель может описывать PRC для осциллятора Стюарта-Ландау [57] и широко используется как каноническая форма PRC вблизи бифуркации Хопфа [58] — [61].Если устойчивая разность фаз для однородной системы равна (противофазный режим), разность фаз для неоднородной системы составляет (15)
Для синхронного случая запаздывание по фазе составляет: (16)
Решения устойчивы, если (17) для первого случая и (18) для второго случая. Результаты для канонических нейронов типа II, а также результаты численного интегрирования уравнений. 12 и 13 показаны на рис. 2b. Видно отличное соответствие численного решения фазовой модели аналитическим результатам линейной аппроксимации.На правых панелях рис. 2 были показаны численные результаты для нейронов HH, демонстрирующие согласие между результатами импульсной фазовой модели с более реалистичной нейронной моделью, основанной на проводимости.
Динамическая ретрансляция
Когда два нейрона взаимодействуют косвенно через третий ретрансляционный нейрон, симметрия системы подразумевает, что как синфазное, так и противофазное срабатывание напрямую связанных нейронов приводит к синхронизации нейронов в противофазном состоянии. Пусть, где нижний индекс обозначает релейный нейрон и маркирует внешние нейроны.Пока внешние нейроны синхронизируются независимо от величины разности фаз внешних нейронов и ретрансляционного нейрона.
В установившемся режиме синхронизации 1∶1 между каждыми двумя последовательными всплесками ретрансляционного нейрона происходит однократный всплеск внешних нейронов. Мы строим карту, записывая фазы трех нейронов во время пиков релейного нейрона: (19) где,.
Сначала исследуем приведенные выше уравнения в однородной сети, где, и. Легко проверить, что синхронное состояние (и) является решением.Для проверки стабильности отметим, что для состояния 1 locked1 фазовой синхронизации, и. Тогда уравнения сводятся к (20), и линейный анализ устойчивости показывает, что синхронное решение устойчиво, если. Интересен тот факт, что, как и в системе двух нейронов, фазовая задержка в мотиве гомогенной релейной системы не зависит от синаптической силы. Например, для нейронов типа II, если принять типичную форму фазовой чувствительности, уравнение. 20 дает. Аналитические результаты для типичных нейронов II типа представлены на рис.5 вместе с численными результатами, полученными при интегрировании уравнений. 8. Можно также увидеть, что изменение временной задержки приводит к трем различным стабильным синхронизированным состояниям с нулевой временной задержкой для внешних нейронов. Ибо около или внешние нейроны полностью синхронизируются, при этом они имеют небольшую разность фаз с релейным узлом. Ибо задержки вокруг внешних нейронов все еще полностью синхронизированы, но почти в противофазе с релейным. Синхронность, наблюдаемая в диапазоне задержки, для которого две системы нейронов показывают противофазную синхронизацию, ожидаема, как отмечалось выше, но для системы трех нейронов существуют интервалы временной задержки, в течение которых режим блокировки 1-1 не является стабильным.Эти области, изображенные заштрихованной областью на рис. 5, имеют значительную меру вокруг того места, где система из двух нейронов имеет набор нейтрально стабильных решений, как обсуждается после уравнения. 14. На правой панели фиг. 5 показаны результаты для системы, состоящей из трех нейронов Ходжкина-Хаксли. Результаты качественно согласуются, но, что интересно, для нейронов HH область нестабильности синхронизированного состояния намного меньше по сравнению с фазовыми осцилляторами. Наши результаты подтверждают, что области синхронизации в пространстве параметров релейной системы зависят от модели осцилляторов и небольшой области асинхронности, наблюдаемой в других исследованиях (см.грамм. [43]) может быть следствием выбора модельных осцилляторов (см. Также [40]). В следующих разделах мы покажем, что области синхронности могут быть расширены в некоторых случаях, используя неоднородности, которые сохраняют симметрию релейной системы.
Рисунок 5. Однородная релейная система.
В однородной релейной системе синхронизированное состояние внешних нейронов не является стабильным для всех значений времени задержки. Темно-синие и голубые точки показывают разность фаз внешних нейронов в стабильных областях, полученную в результате аналитических расчетов и прямого численного интегрирования, соответственно.Темно-розовыми (розовыми) точками показаны аналитические (численные) результаты для разности фаз внешних нейронов с релейным нейроном. Желтые и оранжевые линии показывают характеристический показатель карты, отрицательный в случае устойчивости синхронности. Вертикальные пунктирные линии показывают границу областей устойчивости (характеризующихся отрицательными показателями степени), а заштрихованная область указывает область, в которой численное интегрирование не показывает синхронности. На правой панели представлены численные результаты для релейной системы с нейронами Ходжкина-Хаксли.Примечательно, что, хотя наблюдается тот же самый образец областей синхронизации, но область, в которой синхронизация нестабильна, довольно уже для релейной системы с нейронами HH.
https://doi.org/10.1371/journal.pone.0112688.g005
Неоднородность в динамических релейных системах
Каждый из трех параметров, собственная частота нейронов, синаптическая сила и временные задержки могут быть изменены, чтобы исследовать влияние неоднородности в релейной системе нейронов.Неоднородность может проявляться так, что симметрия системы сохраняется или нет. Например, если частота срабатывания ретрансляционного нейрона отличается от внешних нейронов, система неоднородна, но симметрична, а с другой стороны, если частота срабатывания одного внешнего нейрона отличается от двух других нейронов, система больше не симметрично. Мы предполагаем, что система менее чувствительна к неоднородности, пока симметрия не нарушена. [43] показали, что синхронизация внешних нейронов в динамической релейной системе практически нечувствительна к скорости срабатывания релейного нейрона.Далее мы проверяем влияние неоднородности на синхронность внешних нейронов, изменяя три параметра: скорость возбуждения, задержки передачи и силу синапсов. Для каждого из отмеченных параметров мы проверяем два случая, когда система неоднородна, но симметрична, и когда наложенная неоднородность нарушает симметрию.
Несимметричное рассогласование частоты
Когда частота внешних нейронов не совпадает (нарушена симметрия), больше не является решением уравнения.21 и наружные шипы не появляются одновременно. Это очевидно из рис. 7a, который показывает, что фазовая задержка внешних нейронов непрерывно изменяется с рассогласованием, и только при нулевом рассогласовании может наблюдаться синхронизация нулевой задержки. В этом случае вместо решения с нулевым запаздыванием мы ищем состояние фазовой синхронизации, в котором. Уравнения. 19, то можно записать как (22) где. На рис. 7b также изображено соотношение частот возбуждения нейронов. Область устойчивости фазовой синхронизации (характеризуемой) показана сплошными линиями, что снова хорошо согласуется с численными результатами.Результаты подтверждаются численными экспериментами на нейронах HH, показанными на рис. 7, где можно наблюдать качественно аналогичную зависимость от несовпадения внешних нейронов.
Рисунок 7. Асимметричная релейная система с неоднородной скорострельностью.
Когда рассогласование частоты применяется к одному из внешних нейронов, синхронизированное состояние не наблюдается, но для некоторого диапазона рассогласования возникают состояния с фазовой синхронизацией 1: 1. (а) и (б) показывают фазовую задержку и соотношение периодов внешних нейронов в установившемся состоянии, соответственно.Синие линии — границы мод 1∶1 из теста аналитической устойчивости. Справа такие же результаты показаны для нейронов HH.
https://doi.org/10.1371/journal.pone.0112688.g007
Различные синаптические константы: асимметричный случай
Если соединения на обеих сторонах имеют разную прочность, в соответствии с ур. 19 синхронизированное состояние для внешних нейронов,, в общем, не является решением заданной карты (уравнения 19). В простейшем случае, когда синапсы на одной стороне имеют одинаковую силу, но они немного отличаются от синапсов на другой стороне, возможны состояния, близкие к синхронным.Численные результаты, показанные на рис. 9, представлены для типичных генераторов типа II. Почти синхронные результаты видны, когда или.
Рис. 9. Асимметричное изменение синаптических констант.
Временная задержка срабатывания нейронов показана как функция времени задержки и отношения синаптических констант в случае асимметрии. Численные результаты подтверждают результаты аналитических расчетов фазового запаздывания фазовых осцилляторов II типа (левая панель). Правая панель показывает результаты для нейронов HH.Снова наблюдается синхронизация с нулевой задержкой для и.
https://doi.org/10.1371/journal.pone.0112688.g009
Неоднородные задержки: симметричный случай
В случае неравных задержек передачи, если симметрия сохраняется, то есть входящие и исходящие задержки (и) неравны, но соответствующие линии связи на двух сторонах имеют равные задержки, синхронизация с нулевой задержкой все еще возможна. Наложение в уравнения. 19, фиксированная точка карты определяется и условие устойчивости.Для типичных осцилляторов типа II фазовое отставание внешних нейронов от релейного нейрона составляет.
На рис. 10 показаны численные результаты для канонических осцилляторов II типа. Показана фазовая задержка внешних нейронов для разных значений задержки входящей и исходящей передачи. Сплошные линии показывают границу области, в которой выполняется критерий устойчивости. На правой панели рис. 10 показаны результаты для нейронов HH. Система ведет себя качественно так же, как осцилляторы типа II, но есть области, в которых вместо нулевой фазовой задержки регистрируется очень маленькая фазовая задержка, и, что интересно, для небольшого количества исходящей синаптической временной задержки наблюдается полная синхронность для нейронов HH, независимо от значения входящих синаптических задержек.
Рисунок 10. Симметричное изменение времен задержки.
На левой панели фазовая задержка внешних нейронов в релейной системе с каноническими генераторами II типа. Горизонтальная и вертикальная оси показывают время задержки на входе и выходе соответственно. Сплошные линии показывают границу устойчивой синхронности. Аналогичные результаты показаны для нейронов HH справа.
https://doi.org/10.1371/journal.pone.0112688.g010
Обсуждение
В этом исследовании мы исследовали влияние неоднородности на синхронизацию двух нейронов, которые опосредованно общаются через третий ретрансляционный нейрон.Эта структура была предложена в качестве механизма синхронизации удаленных областей мозга, которые демонстрируют синхронизацию без запаздывания, несмотря на значительную задержку в их коммуникации [39], [41].
Есть несколько экспериментальных доказательств того, что гамма-колебания в широко разделенных областях мозга демонстрируют почти нулевую синхронизацию [10], [65] — [68]. Помимо функциональной значимости, этот результат примечателен, поскольку неясно, как нейроны могут синхронизироваться, несмотря на значительные задержки из-за аксональной проводимости и синаптической передачи.Многие теоретические и численные исследования посвящены исследованию условия синхронизации связанных с запаздыванием осцилляторов [28], [29], [33], [59], [69]. Сейчас хорошо известно, что синхронизация напрямую связанных осцилляторов зависит от их типа возбудимости и в зависимости от кривой фазовой характеристики, и синхронизация возможна для некоторого диапазона времени задержки [33], [56], [70]. Интересно, что для релейной системы синхронизация возможна в гораздо более широком диапазоне времени задержки, независимо от типа возбудимости нейронов [39], [41].
Наиболее важным требованием для синхронизации с нулевым запаздыванием фазы является то, что ретрансляционная популяция клеток занимает временное равноудаленное место от пулов нейронов, которые необходимо синхронизировать [41]. Этот разумный аргумент был сформулирован в нашем настоящем исследовании как более общий вопрос. Как неоднородность влияет на синхронность внешних нейронов в релейной системе? В минимальной ретрансляционной системе три нейронных осциллятора с заданными PRC характеризуются своей частотой срабатывания, а связи — синаптической силой и временем задержки.Изменение каждого из этих параметров может быть источником неоднородности. Что касается критерия, выраженного выше, например, устойчивость системы может быть проверена по разнице между временами задержки для входящих и исходящих синапсов, когда двойники двух крыльев имеют одинаковую задержку. Это пример, в котором неоднородность не нарушает структурную симметрию системы. Мы показали, что такие симметричные неоднородности имеют незначительное влияние на синхронность внешних нейронов и, что интересно, в некоторых случаях это может даже усилить синхронность.В частности, когда входящие синапсы слабее исходящих, синхронность наблюдается в более широком диапазоне задержек.
Мы также показали, что релейная система не является устойчивой к асимметричной неоднородности . Например, если внешние нейроны имеют разные внутренние частоты возбуждения, их фазовая задержка будет иметь конечное значение, которое является возрастающей функцией несоответствия между внутренними частотами возбуждения. В линейном приближении мы дали фазовые запаздывания импульсов внешних нейронов как функцию несоответствия между параметрами двух крыльев, т.е.е., частота возбуждения, синаптическая сила и время задержки. Наши результаты предполагают, что в реальной ретрансляционной системе, где ни нейронные, ни синаптические параметры не настроены точно, можно ожидать почти нулевой задержки вместо точной синхронизации. В нервной системе частота возбуждения непостоянна, и синаптическая эффективность меняется из-за краткосрочной и долгосрочной пластичности. Нейрональные и синаптические изменения в коротких временных масштабах могут привести к появлению временной синхронности, о которой сообщалось в различных экспериментах с сенсорными системами [71] — [73].Долгосрочные изменения в силе синапсов могут также влиять на коллективные свойства нейронных сетей [см., Например, [74] — [76], и необходимы дальнейшие исследования, чтобы выявить роль синаптической пластичности в динамике релейной системы.
Благодарности
Авторы выражают благодарность Магтельду Цайтлеру, Клаудио Р. Мирассо и Горацио Г. Ротштейну за чтение рукописи и ценные комментарии.
Вклад авторов
Задумал и спроектировал эксперименты: ZGE AV.Проведены эксперименты: ЗГЭ А.В. Проанализированы данные: ЗГЭ А.В. Предоставленные реагенты / материалы / инструменты анализа: ZGE AV. Написал статью: ЗГЭ А.В.
Ссылки
- 1.
Murphy J, Kwan H, Wong Y (1985) Исследования взаимной корреляции в моторной коре приматов: синаптическое взаимодействие и совместный ввод. Канадский журнал неврологических наук Le journal canadien des Sciences Neurologiques 12: 11–23. - 2.
Gray CM, König P, Engel AK, Singer W (1989) Колебательные ответы в зрительной коре головного мозга кошек демонстрируют межколоночную синхронизацию, которая отражает глобальные свойства стимула.Природа 338: 334–337. - 3.
Vaadia E, Aertsen A (1992) Кодирование и вычисления в коре: активность одного нейрона и кооперативные явления. В: Обработка информации в коре, Springer. С. 81–121. - 4.
Силлито AM, Jones HE, Gerstein GL, West DC (1994) Связанная с особенностями синхронизация активации таламических ретрансляционных клеток, вызванная обратной связью от зрительной коры. Природа 369: 479–482. - 5.
Riehle A, Grün S, Diesmann M, Aertsen A (1997) Синхронизация спайков и модуляция скорости по-разному участвуют в моторной корковой функции.Science 278: 1950–1953. - 6.
Steriade M, Contreras D (1998) Спайк-волновые комплексы и быстрые компоненты корковых приступов i. роль неокортекса и таламуса. Журнал нейрофизиологии 80: 1439–1455. - 7.
Цодыкс М., Узиэль А., Маркрам Х. (2000) Генерация синхронности в рекуррентных сетях с частотно-зависимыми синапсами. J Neurosci 20: 825–835. - 8.
Трауб Р.Д. (1999) Быстрые колебания в корковых цепях. MIT press - 9.Gray CM, Engel AK, König P, Singer W (1990) Стимул-зависимые нейронные колебания в зрительной коре кошек: свойства рецептивного поля и зависимость характеристик. Европейский журнал нейробиологии 2: 607–619.
- 10.
Roelfsema PR, Engel AK, Konig P, Singer W (1997) Визуомоторная интеграция связана с нулевой временной задержкой синхронизации между корковыми областями. Природа 385: 157–161. - 11.
Трауб Р. Д., Уиттингтон М. А., Стэнфорд И. М., Джефферис Дж. Г. (1996) Механизм генерации синхронных быстрых колебаний на большие расстояния в коре головного мозга.Природа 383: 621–624. - 12.
Contreras D, Destexhe A, Sejnowski TJ, Steriade M (1996) Контроль пространственно-временной когерентности таламических колебаний с помощью кортикоталамической обратной связи. Наука 274: 771–774. - 13.
Фрис П. (2009) Нейронная гамма-полосная синхронизация как фундаментальный процесс корковых вычислений. Ежегодный обзор нейробиологии 32: 209–224. - 14.
Womelsdorf T, Fries P (2007) Роль нейрональной синхронизации в избирательном внимании.Текущее мнение в нейробиологии 17: 154–160. - 15.
Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W., Desimone R, et al. (2007) Модуляция взаимодействий нейронов посредством синхронизации нейронов. наука 316: 1609–1612. - 16.
Фрис П. (2005) Механизм когнитивной динамики: нейронная связь через нейронную когерентность. Тенденции в когнитивных науках 9: 474–480. - 17.
Бузаки Г. (2006) Ритмы мозга. Oxford University Press - 18.Бужаки Г., Драгун А. (2004) Нейронные колебания в корковых сетях. Наука 304: 1926–1929.
- 19.
Ван XJ, Buzsáki G (1996) Гамма-осцилляция за счет синаптического торможения в модели межнейрональной сети гиппокампа. Журнал неврологии 16: 6402–6413. - 20.
Mirollo RE, Strogatz SH (1990) Синхронизация биологических осцилляторов с импульсной связью. Журнал SIAM по прикладной математике 50: 1645–1662. - 21.
Брунель Н., Хаким В. (1999) Быстрые глобальные колебания в сетях интегрированных и запускаемых нейронов с низкой частотой срабатывания.Нейронные вычисления 11: 1621–1671. - 22.
Чавес М., Хванг Д., Аманн А., Хентшель Н., Боккалетти С. и др. (2005) Синхронизация улучшена в взвешенных сложных сетях. Phys Rev Lett 94: 218701. - 23.
Börgers C, Kopell N (2003) Синхронизация в сетях возбуждающих и тормозных нейронов с редкими случайными связями. Нейронные вычисления 15: 509–538. - 24.
Лу В., Чен Т. (2004) Синхронизация связанных связанных нейронных сетей с задержками.IEEE Transactions on Circuits and Systems Part 1: Regular Papers 51: 2491–2503. - 25.
D’Huys O, Vicente R, Danckaert J, Fischer I (2010) Синхронизация и нарушение симметрии осцилляторов с запаздыванием: о роли фазовой и амплитудной нестабильности. В: SPIE Photonics Europe. Международное общество оптики и фотоники, стр. 772023–772023. - 26.
Энглерт А., Кинзель В., Авиад Ю., Бутковски М., Рейдлер И. и др. (2010) Синхронизация хаотических систем без запаздывания с запаздывающими связями.Письма о физическом осмотре 104: 114102. - 27.
Flunkert V, Yanchuk S, Dahms T, Schöll E (2010) Синхронизация удаленных узлов: универсальная классификация сетей. Письма физического обзора 105: 254101. - 28.
Ernst U, Pawelzik K, Geisel T (1995) Синхронизация, вызванная временными задержками в генераторах с импульсной связью. Письма физического обзора 74: 1570. - 29.
Ernst U, Pawelzik K, Geisel T (1998) Мультистабильная синхронизация биологических осцилляторов, вызванная задержкой.Физический обзор E 57: 2150. - 30.
Ван Фрисвейк К., Эбботт Л., Эрментроут Г.Б. (1994) Когда торможение, а не возбуждение, синхронизирует нервное возбуждение. Журнал вычислительной нейробиологии 1: 313–321. - 31.
Smeal RM, Ermentrout GB, White JA (2010) Кривые фазового отклика и синхронизированные нейронные сети. Философские труды Королевского общества B: Биологические науки 365: 2407–2422. - 32.
Эрментроут Г.Б., Гласс Л., Олдеман Б.Е. (2012) Форма кривых восстановления фазы в осцилляторах с седловидным узлом на бифуркации инвариантной окружности.Нейронные вычисления 24: 3111–3125. - 33.
Achuthan S, Canavier CC (2009) Кривые сброса фазы определяют синхронизацию, фазовую синхронизацию и кластеризацию в сетях нейронных осцилляторов. Журнал неврологии 29: 5218–5233. - 34.
Ermentrout B (1996) Мембраны типа i, кривые восстановления фазы и синхронность. Нейронные вычисления 8: 979–1001. - 35.
Canavier CC (2006) Кривая фазовой характеристики. Scholarpedia 1: 1332. - 36.
Ижикевич Е.М. (2006) Полихронизация: вычисление с пиками.Нейронные вычисления 18: 245–282. - 37.
Ermentrout B, Pascal M, Gutkin B (2001) Влияние адаптации частоты всплесков и отрицательной обратной связи на синхронизацию нейронных осцилляторов. Нейронные вычисления 13: 1285–1310. - 38.
Ermentrout GB, Beverlin II B, Netoff T (2012) Кривые фазового отклика для измерения воздействия ионных каналов на нейроны. В: Кривые фазовой реакции в неврологии, Springer. С. 207–236. - 39.
Фишер И., Висенте Р., Булду Дж. М., Пейл М., Мирассо С. Р. и др.(2006) Долгосрочная синхронизация с нулевой задержкой посредством динамической ретрансляции. Письма о физическом осмотре 97: 123902. - 40.
Viriyopase A, Bojak I, Zeitler M, Gielen S (2012) Когда в корковых сетях возможна долгосрочная синхронизация с нулевой задержкой. Границы вычислительной нейробиологии 6. - 41.
Висенте Р., Фишер И., Мирассо К.Р. (2008) Синхронизирующие свойства трех полупроводниковых лазеров с запаздыванием. Physical Review E 78: 066202. - 42.
Голло Л.Л., Мирассо С., Спорнс О, Брейкспир М. (2014) Механизмы синхронизации без запаздывания в корковых мотивах.Вычислительная биология PLoS 10: e1003548. - 43.
Vicente R, Gollo LL, Mirasso CR, Fischer I, Pipa G (2008) Динамическая ретрансляция может дать нейронную синхронизацию с нулевым запаздыванием, несмотря на длительные задержки проводимости. Труды Национальной академии наук 105: 17157–17162. - 44.
Голло Л.Л., Мирассо С., Вилла А.Е. (2010) Динамический контроль для синхронизации разделенных областей коры через таламическое реле. Нейроизображение 52: 947–955. - 45.
Young CK, McNaughton N (2009) Связь тета-колебаний между передней и задней срединной корой и с гиппокампом у свободно ведущих крыс.Кора головного мозга 19: 24–40. - 46.
Murthy VN, Fetz EE (1992) Когерентные колебания от 25 до 35 Гц в сенсомоторной коре головного мозга бодрствующих обезьян. Труды Национальной академии наук 89: 5670–5674. - 47.
Bland BH, Oddie SD (2001) Колебания и синхронность тета-диапазона в формировании гиппокампа и связанных с ним структурах: аргумент в пользу его роли в сенсомоторной интеграции. Поведенческое исследование мозга 127: 119–136. - 48.
Honey CJ, Kötter R, Breakspear M, Sporns O (2007) Сетевая структура коры головного мозга формирует функциональную связность во многих временных масштабах.Труды Национальной академии наук 104: 10240–10245. - 49.
Sporns O, Kötter R (2004) Мотивы в сетях мозга. PLoS биология 2: e369. - 50.
Gollo LL, Mirasso CR, Atienza M, Crespo-Garcia M, Cantero JL (2011) Кортикальная синхронизация с нулевой задержкой и дальней корковой синхронизацией с тета-диапазоном через динамическую ретрансляцию гиппокампа. PloS one 6: e17756. - 51.
Барбур Б., Брунель Н., Хаким В., Надаль Дж. П. (2007). Что мы можем узнать из синаптических весовых распределений? ТЕНДЕНЦИИ в неврологии 30: 622–629. - 52.
Roxin A, Brunel N, Hansel D, Mongillo G, van Vreeswijk C (2011) О распределении частоты возбуждения в сетях корковых нейронов. Журнал неврологии 31: 16217–16226. - 53.
Панчук А., Розин Д. П., Хёвель П., Шёлль Э (2013) Синхронизация связанных нейронных осцилляторов с неоднородными задержками. Международный журнал бифуркаций и хаоса 23. - 54.
Эрментрут Г.Б., Терман Д.Х. (2010) Математические основы нейробиологии, том 64.Спрингер - 55.
Ижикевич Е.М. (2007) Динамические системы в нейробиологии. МИТ пресс - 56.
Садеги С., Вализаде А. (2014) Синхронизация запаздывающих связанных нейронов при наличии неоднородности. Журнал вычислительной нейробиологии 36: 55–66. - 57.
Терамае Дж., Танака Д. (2004) Устойчивость индуцированной шумом фазовой синхронизации в общем классе генераторов с предельным циклом. Письма о физическом обзоре 93: 204103. - 58.
Ariaratnam JT, Strogatz SH (2001) Фазовая диаграмма беспроигрышной модели связанных нелинейных осцилляторов.Письма физического обзора 86: 4278. - 59.
Goel P, Ermentrout B (2002) Синхронность, стабильность и схемы срабатывания в генераторах с импульсной связью. Physica D: нелинейные явления 163: 191–216. - 60.
Brown E, Moehlis J, Holmes P (2004) О сокращении фазы и динамике отклика популяций нейронных осцилляторов. Нейронные вычисления 16: 673–715. - 61.
Hansel D, Mato G, Pfeuty B (2012) Роль внутренних свойств клетки в синхронизации нейронов, взаимодействующих через электрические синапсы.В: Кривые фазовой реакции в неврологии, Springer. С. 361–398. - 62.
Брейман Й., Линднер Дж. Ф., Дитто В. Л. (1995) Укрощение пространственно-временного хаоса беспорядком. Природа 378: 465–467. - 63.
Valizadeh A, Kolahchi M, Straley J (2010) Узел перехода с одной фазой скольжения может синхронизировать параллельный сверхпроводящий массив линейно связанных джозефсоновских переходов. Physical Review B 82: 144520. - 64.
Банерджи Р., Гош Д., Падманабан Э., Рамасвами Р., Пекора Л. и др.(2012) Повышение синхронности хаотических генераторов с помощью динамической ретрансляции. Physical Review E 85: 027201. - 65.
Frien A, Eckhorn R, Bauer R, Woelbern T, Kehr H (1994) Специфичные для стимула быстрые колебания в нулевой фазе между визуальными областями v1 и v2 бодрствующей обезьяны. Нейроотчет 5: 2273–2277. - 66.
Кастело-Бранко М., Нойеншвандер С., Сингер В. (1998) Синхронизация зрительных ответов между корой, латеральным коленчатым ядром и сетчаткой у обезболенной кошки.Журнал неврологии 18: 6395–6410. - 67.
Родригес Э., Джордж Н., Лашо Дж. П., Мартинери Дж., Рено Б. и др. (1999) Тень восприятия: удаленная синхронизация мозговой активности человека. Природа 397: 430–433. - 68.
Гросс Дж., Шмитц Ф., Шницлер И., Кесслер К., Шапиро К. и др. (2004) Модуляция нервной синхронизации на большие расстояния отражает временные ограничения зрительного внимания у людей. Труды Национальной академии наук Соединенных Штатов Америки 101: 13050–13055. - 69.
Йунг М.С., Строгац С.Х. (1999) Временная задержка в модели связанных осцилляторов Курамото. Physical Review Letters 82: 648. - 70.
Вудман М.М., Канавье С.К. (2011) Влияние задержек проводимости на существование и стабильность однофазной синхронизации между двумя генераторами с импульсной связью. Журнал вычислительной нейробиологии 31: 401–418. - 71.
Gray CM, Singer W (1989) Стимул-специфические нейрональные колебания в ориентационных столбцах зрительной коры головного мозга кошки.Труды Национальной академии наук 86: 1698–1702. - 72.
Баженов М., Стопфер М., Рабинович М., Хуэрта Р., Абарбанель HD и др. (2001) Модель временной колебательной синхронизации в антеннальной лопасти саранчи. Нейрон 30: 553–567. - 73.
Фридрих RW, Habermann CJ, Laurent G (2004) Мультиплексирование с использованием синхронизации в обонятельной луковице рыбок данио. Природа нейробиологии 7: 862–871. - 74.
Карбовски Дж., Эрментроут Г.Б. (2002) Синхронность, возникающая из сбалансированной синаптической пластичности в сети гетерогенных нейронных осцилляторов.Physical Review E 65: 031902. - 75.
Новотный Т., Жигулин В.П., Селверстон А.И., Абарбанель Х.Д., Рабинович М.И. (2003) Повышение синхронизации в гибридной нейронной цепи за счет пластичности, зависящей от времени спайков. Журнал неврологии 23: 9776–9785. - 76.
Баяти М., Вализаде А. (2012) Влияние синаптической пластичности на структуру и динамику неупорядоченных сетей связанных нейронов. Physical Review E 86: 011925.
границ | Когда возможна длительная синхронизация с нулевым запаздыванием в корковых сетях
Введение
Связь между различными осцилляторами и кардиостимуляторами может генерировать широкий спектр различного поведения и была предметом изучения во многих различных условиях, например, при кардиостимуляции и химических колебаниях (см. E.г., Goldbeter, 1996; Кох, Сегев, 1998; Роксин и др., 2005). Особым случаем является взаимодействие между нейронами, которое вызывает колебания нейронов в определенных частотных диапазонах. Синхронизация нейронного гамма-диапазона была описана у многих видов и в большом количестве структур мозга для решения различных сенсорных и моторных задач (Gray et al., 1989; Fries et al., 2001, 2008; Pesaran et al., 2002; Schoffelen et al., 2005). Эта крупномасштабная синхронизация нескольких корковых областей была постулирована как потенциальный механизм интеграции и координации нейрональной активности в когнитивных задачах (Engel et al., 1992; Певец и Грей, 1995; Фрис, 2005).
Первые исследования по этой теме представили экспериментальные доказательства того, что относительная фаза гамма-колебаний в широко разделенных областях мозга близка к нулю (Frien et al., 1994; Roelfsema et al., 1997; Castelo-Branco et al., 1998; Rodriguez et al., 1999; Gross et al., 2004). Этот результат был замечательным, поскольку синхронизация требует взаимодействия между удаленными областями мозга, которое происходит со значительными задержками из-за аксональной проводимости и синаптической передачи.Поэтому многие дальнейшие исследования изучали, как удаленные колебательные области мозга могут синхронизироваться с нулевой задержкой, несмотря на заметные задержки. В нескольких теоретических исследованиях утверждается, что прямая взаимная импульсная связь между двумя динамическими системами с задержками и возбуждающими синапсами не может легко привести к синхронизации с нулевым запаздыванием (Ernst et al., 1995, 1998; Goel and Ermentrout, 2002; Zeitler et al., 2009 ). Таким образом, Fischer et al. (2006) и Vicente et al. (2008) предположили, что синхронизация без запаздывания между областями мозга может быть опосредована третьим (релейным) осциллятором.Потенциальным кандидатом на роль этого генератора-ретранслятора нейронов является таламус (Gollo et al., 2010; Theyel et al., 2010).
Чтобы лучше понять возможности синхронизации удаленных областей мозга с нулевой задержкой, мы исследовали предложенную сеть нейронных осцилляторов, косвенно связанных релейным осциллятором (Fischer et al., 2006; Vicente et al., 2008). ). Мы исследовали модель как с нейронами Миролло – Строгаца I типа, так и с нейронами Ходжкина – Хаксли II типа.Мы сосредоточились, в частности, на устойчивости нулевой фазовой синхронизации как функции времени задержки между осцилляторами и силы синаптической связи. Были исследованы различные типы синаптического взаимодействия, в том числе пластичность, зависящая от времени спайка (STDP), поскольку предполагается, что STDP способствует эффективной передаче информации (Buonomano and Maass, 2009; Lindner et al., 2009; Hennequin et al., 2010). . Наши результаты показывают, что возможна синхронизация с нулевым запаздыванием, особенно для моделей с нейронами типа II Ходжкина – Хаксли.STDP обеспечивает синхронизацию с нулевым запаздыванием, поскольку STDP изменяет синаптическую силу и тем самым допускает больший диапазон начальных синаптических сил, которые могут привести к синхронизации с нулевой задержкой.
Материалы и методы
Модель состоит из трех связанных нейронных осцилляторов (см. Рисунок 1A). Каждый осциллятор можно рассматривать как отдельный нейрон или как совокупность нейронов, где предполагается, что активность нейронов в каждой популяции однородна и высоко синхронизирована.Как показано на рисунке 1A, «реле» или «внутренний» генератор (генератор 2) двунаправленно связан с двумя «внешними» генераторами (генераторами 1 и 3). Внешние генераторы связаны только с релейным генератором, но не напрямую друг с другом. В качестве отправной точки мы предполагаем, что все три генератора идентичны с одинаковым внутренним периодом срабатывания T 0 .
Рис. 1. Схема модели и ее режим синхронизации без запаздывания 1: 1 с фазовой синхронизацией . (A) Схема генераторов 1 и 3 с двунаправленной связью импульсов через релейный генератор 2. ε ij представляет возбуждающую синаптическую нагрузку от генератора j к генератору i , τ k задержка проводимости между релейным генератором 2 и генератором k . (B) Пример режима синхронизации с нулевой задержкой и синхронизацией по фазе 1: 1. Вертикальные полосы представляют время всплеска осцилляторов. T 0 — собственный период генераторов, T < T 0 — общий период генераторов в режиме фазовой синхронизации, а θ T — задержка между срабатыванием реле. и внешние осцилляторы.t1, nspike, t2, nspike и t3, nspike — это n -ое время всплеска осцилляторов 1, 2 и 3 соответственно.
Мы использовали фазовый осциллятор Миролло – Строгаца (MS) (Mirollo and Strogatz, 1990) и классический нейрон Ходжкина и Хаксли (HH) (Hodgkin and Huxley, 1952) с параметрами, приведенными в Vicente et al. (2008). Для фазового генератора MS T 0 выбрано равным 25 мс, а T 0 нейрона HH составляет 14,66 мс с параметрами, приведенными в Vicente et al.(2008). На рисунке 1A ε ij представляет силу связи от пресинаптического осциллятора j к постсинаптическому осциллятору i . Все синаптические связи в модели являются возбуждающими. Время задержки τ k представляет время проведения спайков вдоль аксонов, которые соединяют осциллятор k с релейным генератором. Здесь мы делаем упрощающее предположение, что времена задержки постоянны и симметричны (т.е. время задержки от генератора i до j равно времени задержки от генератора j до i ).Эти времена задержки обычно значительно короче, чем период нейронных колебаний (Fries, 2005). Поэтому в дальнейшем мы будем рассматривать только задержки проводимости меньше, чем T 0 /2, при этом τ k выражается как часть собственного периода T 0 и, следовательно, находится в диапазоне от 0 до 0,5.
Генератор фазы MS (Mirollo and Strogatz, 1990) характеризуется переменной состояния, подобной напряжению f ∈ [0, 1], которая монотонно увеличивается от 0 до порогового значения f = 1.В пределах цикла состояние несвязанного нейронального осциллятора определяется монотонно возрастающей вогнутой функцией f (φ): [0, 1] → [0, 1]:
f (φ) = 1bln1 + eb-1φ, (1) dφdt = 1T0, (2)
с фазовой переменной φ ∈ [0, 1] и параметром рассеяния b . T 0 — собственный период срабатывания генератора. При достижении порога генератор срабатывает, переменная состояния f сбрасывается в ноль, и цикл повторяется.Как и у Ernst et al. (1995) и Zeitler et al. (2009), в данном исследовании используется настройка b = 3. Нейрон МС — это так называемый нейрон I типа (Ижикевич, 2007), где возбуждающий сигнал всегда дает сдвиг фазы нейронного осциллятора.
Для классического нейрона HH мембранный потенциал В определяется дифференциальным уравнением:
CdVdt = -gNam3hV-ENa-gKn4V-EK-gLV-EL + Iext + Isyn, (3)
с емкостью мембраны C и максимальной проводимостью натрия г Na , калия г K и утечки г л .Соответствующие реверсивные потенциалы ( E Na , E K , E L ) и внешний ток I ext приведены в Vicente et al. (2008). Управляемые по напряжению ионные каналы m, h и n описываются дифференциальными уравнениями первого порядка. Обратите внимание, что выражение для α n в Vicente et al. (2008) неверно и должно выглядеть следующим образом: α n ( V ) = [( V + 55) / 100] / {1 — exp [- 0.1 ( В, + 55)]}. Возбуждающий синаптический ток I syn равен −ε ij S ( t ) V , где ε ij — максимальная синаптическая проводимость, а S ( t ) — дельта-функция Дирака (в случае «мгновенного синапса») или альфа-функция (в случае «альфа-синапса»). Этот классический нейрон HH представляет собой нейрон так называемого типа II (Ижикевич, 2007), где возбуждающее воздействие на ранних фазах цикла активации вызывает задержку фазы, но сдвиг фазы в более поздних фазах цикла активации.
Синаптическая муфта
Мы исследуем две модели импульсной связи между генераторами. Для мгновенного синапса с силой связи ε ij состояние нейрона f i фазового осциллятора MS после прихода импульса от осциллятора j увеличивается мгновенно
finewφi = minfiφi + εij, 1, (4)
с φ i фазой постсинаптического осциллятора i в момент прихода спайка.Фаза φ i , для которой осциллятор достигает порога после ввода пика [т.е. f i (φ i ) + ε ij = 1], называется критической фазой. φ c (Zeitler et al., 2009) и определяется как
φcεij = eb1-εij-1eb-1. (5)
Если пик достигает φ i <φ c , f i мгновенно увеличится на ε ij .Мгновенное изменение состояния f i на ε ij соответствует фазовому сдвигу Δφi = fi-1fi (φi) + εij-φi, что дает
Δφiφiεij = χbεij + βbεijφifor0≤φi <φc1-φiforφc≤φi <1, (6)
с
χbx≡βbxβb1, βbx≡ebx-1, (7)
, где φ i — фаза постсинаптического осциллятора непосредственно перед приходом входного пика. Обратите внимание, что φ c (ε ij ) = [1 — χ b (ε ij )] / [1 + β b (ε ij )].
Цубо и др. (2007) измерили фазовые сдвиги пирамидных нейронов слоя 5 и слоя 2/3 в моторной коре головного мозга крысы. Максимумы усредненных фазовых сдвигов оказались во второй половине колебательного периода для этих нейронов на всех частотах (включая гамма-диапазон; см. Их рисунок 4). Следовательно, мы требуем здесь, чтобы максимум фазового сдвига Δφ i находился во второй части собственного цикла генератора, и, следовательно, φ c > 0.5. Это ограничение накладывает верхнюю границу ε ij <1 - ln [(1 + e b ) / 2] / b = 0,21 для b = 3 на синаптическую силу через Уравнение 5. В случае ε ij = 0,21, всплеск может вызвать увеличение переменной состояния f примерно на 21% разницы между состоянием покоя f = 0 и пороговым значением f = 1. Для нейрона HH верхняя граница максимальной синаптической проводимости равна 3.15 мСм / см 2 , что соответствует увеличению на 21% ( В начало — В покой ), поскольку потенциал покоя В покой и начало потенциала действия В начало находятся около -65 и -50 мВ, соответственно.
Более реалистичная модель синаптического взаимодействия обеспечивается так называемой альфа-функцией. Для «альфа-синапса» постсинаптический потенциал после появления спайка в момент времени t 0 в синапсе с силой ε ij описывается
αtεij, τsyn = 0fort
Пластичность, зависящая от времени всплеска
В общем, сила синаптического взаимодействия непостоянна, но изменяется в зависимости от пре- и постсинаптической активности из-за STDP (Hebb, 1949; Bi and Poo, 1998).Мы реализовали аддитивное правило STDP (Froemke et al., 2006) как для мгновенных, так и для альфа-синапсов. Для пресинаптического спайка во время прибытия tkarr и постсинаптического спайка на tlspike фракционная синаптическая модификация W (Δ t ) дается как
.
WΔt≡A-expΔtτ-forΔt <00forΔt = 0, A + exp-Δtτ + дляΔt> 0 (9)
с Δt≡tlspike-tkarr.
Время прихода спайка tkarr определяется как время начала постсинаптического потенциала, как в экспериментальном протоколе Bi and Poo (1998).Если не указано иное, постоянные времени для потенцирования τ + и депрессии τ — равны τ +, 0 ≡ 16,8 мс и τ -, 0 ≡ 33,7 мс, соответственно. В этом исследовании стандартные значения максимальной амплитуды потенциации A + и депрессии A — составляют A +, 0 ≡ 0,78 и A -, 0 ≡ −0,27, соответственно. Эти стандартные значения параметров для STDP были подогнаны к данным Bi and Poo (1998), которые определили дробную синаптическую модификацию W как относительное изменение синаптической силы после вызова пары входных и выходных спайков 60 раз.Мы предполагаем, что изменение синаптического веса Δε, вызванное каждым входным спайком, является постоянным и определяется как Δε = ε 0 W (Δ t ) / 60 (Song et al., 2000; van Rossum et al. , 2000) с начальным синаптическим весом ε 0 и W (Δ t ), как в уравнении. 9. Таким образом, используемое здесь правило обучения для конкретной пары пре- и постсинаптических спайков задается следующим образом: ε 0 → ε 0 + ε 0 W (Δ t ) / 60, в согласии с Lee et al.(2009).
Процедура моделирования сети для STDP выглядит следующим образом: эволюция состояния сети изучается в течение 60 последовательных сеансов. В начале каждого сеанса начальные фазы трех осцилляторов выбираются произвольно из равномерного случайного распределения. Первый сеанс начинается с равной силы связи для всех синапсов, которая затем изменяется из-за STDP. Все последующие сеансы начинаются с силы связи, полученной в конце предыдущего сеанса, но с повторной рандомизации фаз осцилляторов, чтобы предотвратить схождение системы в локальном, а не глобальном стабильном состоянии.
Чтобы быть физиологически значимым для синхронизации, конвергенция не должна занимать слишком много времени. Поэтому мы предполагаем, что сходимость к устойчивой относительной фазе между осцилляторами 1 и 3 в модели происходит в течение сеанса, состоящего из n ses = 15 циклов. Таким образом, с помощью STDP мы обычно запускаем 60 сеансов по 15 циклов в каждом, чтобы исследовать сходимость сети в стабильном состоянии синхронизации. Без STDP соединения не меняются, и используется один сеанс из 15 циклов.Чтобы избежать ложной зависимости от случайных начальных фаз, мы повторяем каждый расчет 35 3 = 45 875 раз. Таким образом, в случае STDP вычисляется почти 40 миллионов циклов для каждой выбранной настройки силы связи и времени задержки.
Уравнение фазовой синхронизации и анализ устойчивости
Уравнения фазовой синхронизации полезны для определения нового периода сети и относительных фаз связанных осцилляторов (van Vreeswijk et al., 1994; Bressloff and Coombes, 1998).Для простого генератора фазы MS уравнение синхронизации может быть получено аналитически. Полный анализ нашей модели представлен в Приложении, где мы выводим отношения между синаптическим весом, задержкой проводимости и новым периодом осцилляторов для срабатывания внешних осцилляторов с фазовой синхронизацией 1: 1 с нулевой задержкой. Здесь мы просто рассмотрим простой пример (см. Рисунок 1B).
Без ограничения общности, мы устанавливаем время ( n −1) -го срабатывания ретрансляционного нейрона t2, n-1spike = 0 и называем период 1: 1 осцилляторов с фазовой синхронизацией T .Для синхронизации с нулевым запаздыванием существует þeta ∈ [0, 1) такое, что внешние осцилляторы срабатывают при t1, n-1spike = t3, n-1spike = θT, t1, nspike = t3, nspike = θT + T и т. Д. При равных задержках τ 1 = τ 3 = τ, оба всплеска от внешних генераторов достигают релейного генератора в фазе τ + θ T / T 0 (если τ + θ T / T 0 ≤ T / T 0 ) с силой возбуждающей связи ε. Два синаптических входа уменьшают период релейного генератора с собственного периода T 0 до
T = T0 [1 — Δφ (τ + θT / T0 | 2ε)], (10)
с Δφ, как определено в формуле.6. Поскольку релейный нейрон срабатывает при T , каждый из внешних осцилляторов получит пик на T + τ T 0 . Внешние нейроны имеют пик при θ T и, следовательно, их фаза будет τ + (1 — θ) T / T 0 (если τ + (1 — θ) T / T 0 ≤ T / T 0 ) при поступлении импульса от ретрансляционного нейрона. Следовательно, период внешних осцилляторов равен
.
T = T0 [1 — Δφ (τ + (1 — θ) T / T0 | ε)].(11)
Уравнения 10 и 11 представляют собой уравнения синхронизации 1: 1 для упомянутых условий.
Предположим теперь, что обе фазы прихода превышают критические фазы φ c (2ε) и φ c (ε), соответственно. Затем переписав уравнения 10 и 11, используя уравнение. 6 урожаев
T = τT0 + θT и T = τT0 + (1 − θ) T⇒T = 2τT0, θ = 1/2. (12)
Таким образом, период всех осцилляторов вдвое превышает задержку проводимости, и активность переключается между внутренними и внешними осцилляторами каждые полупериод.Все осцилляторы сразу же подскакивают при вводе пика. Мы будем называть этот режим режимом «управляемой синхронизации» (DS) (см. Рисунок 2B). Два других типичных режима также проиллюстрированы на рисунке 2: «подчиненная синхронизация», когда только релейный генератор подает импульс сразу после входа, и «синхронизация кардиостимулятора», когда это делают только внешние генераторы.
Рисунок 2. Особенности синхронизации в зависимости от времени задержки и силы связи . (A) Качество синхронизации (SQ) и (C) Скорость сходимости (CP) для модели с мгновенными синапсами.Толстые черные линии в (A, C) указывают границы динамики, рассчитанные аналитически с использованием уравнения фазовой синхронизации. (B) Иллюстрация режимов синхронности, доминирующих в областях, обозначенных римскими цифрами в (A, C) . SQ высокий в регионе I, низкий в регионах II и IV и средний в регионе III. Подчиненная синхронизация (области II и IV) нестабильна, тогда как ведомая (область I) и синхронизация пейсмейкера (область III) асимптотически стабильны. CP является самым высоким в области I, что указывает на синхронизацию в течение примерно четырех циклов.
Для исследования устойчивости ДС мы предполагаем малые возмущения. Поскольку мы используем всплески релейных нейронов в качестве опорного времени, возмущение влияет на фазу внешних осцилляторов до (τ + δφ 1 , τ + δφ 3 ) в t2, n-1spike. DS является асимптотически устойчивым, если существует δ> 0 такое, что фазы внешних осцилляторов 1 и 3 будут ближе к τ при следующем всплеске в момент t2, nspike для δφ12 + δφ32 <δ. Поскольку φ c (ε) <2τ, мы можем определить значение δ ≡ 2τ - φ c (ε)> 0, и, таким образом, φ c (ε) = 2τ — δ.Всплеск от реле возникает, когда фаза генератора 1 находится в диапазоне 2τ — δ <φ 1 <2τ + δ, что превышает эту критическую фазу φ c (ε). Поэтому осциллятор 1 сразу после получения входного сигнала от ретрансляционного нейрона, и то же самое верно для осциллятора 3. Таким образом, идеальная синхронизация восстанавливается до тех пор, пока возмущение было достаточно небольшим, что доказывает, что режим DS является асимптотически устойчивым режимом. Чтобы определить стабильность других режимов синхронизации, необходимо вычислить собственные значения λ якобиана карты (фазового) возврата (Zeitler et al., 2009), подробности см. В Приложении.
Теперь мы кратко рассмотрим влияние STDP на синхронность ведомого устройства. Сила связи между внешними генераторами и релейным генератором остается неизменной для ведомой синхронизации, поскольку релейный генератор немедленно подскакивает при вводе от внешних нейронов. В Приложении мы показываем, что сила связи между релейным генератором и внешними генераторами увеличивается с ε n > ε n — 1 для τ ≥ 0.25 с использованием окна STDP W (Δ t ) уравнения. 9, поскольку импульс от релейного генератора приходит задолго до импульса внешних нейронов. Следовательно, синаптические веса увеличиваются до φc − 1 (2τ) = 1 − ln [2τ (eb − 1) +1] / b, и в этот момент внешние осцилляторы также вспыхивают сразу после ввода и остановки STDP. Таким образом, STDP превращает ведомую синхронизацию в DS.
В ведомом, кардиостимуляторе и ведомом режимах синхронизации генераторы 1 и 3 генерируют импульс одновременно. Существуют и другие асинхронные стабильные режимы, в которых это не так.На рисунках 3C, D показана динамика осцилляторов для типичного асинхронного случая. Этот режим будет называться «ведомый кардиостимулятор», потому что реле управляет генератором 1 и управляется генератором 3.
Рисунок 3. Преобладание ненулевых относительных фаз . (A) Нормализованная гистограмма относительной фазы φ r для стабильных состояний с τ = 0,25 и ε = 0,1. Примерно для 90% возможных начальных фаз система сходится к ненулевой относительной фазе. (B) | φ r | В зависимости от задержки проводимости τ и синаптического веса ε со средними значениями, проецируемыми на боковые панели. | φ r | уменьшается при увеличении ε и имеет максимум при τ около 0,2. (C, D) Динамика синхронизации «кардиостимулятор-ведомый», соответствующая ненулевой относительной фазе. Сплошные линии представляют время всплеска для значений параметров τ = 0,25 и ε = 0,1, пунктирные линии — для более сильного синаптического веса ε = 0,14 в (C) и большего времени задержки τ = 0.35 в (D) соответственно.
Меры по синхронизации
Для правильного анализа синхронного срабатывания требуется количественное определение синхронности. В экспериментах идеальная синхронность никогда не будет наблюдаться, поскольку шум вызывает небольшие изменения во времени потенциалов действия. Вместо этого мы определим синхронность как срабатывание двух осцилляторов в небольшом временном окне, где временное окно должно быть достаточно большим, чтобы устранить влияние шума, и достаточно маленьким, чтобы обеспечить точную оценку синхронности.Хотя здесь мы можем измерить синхронность в пределах числовой точности нашего моделирования, мы определяем синхронность как условие, когда всплески внешних осцилляторов возникают в пределах t1, nspike-t3, nspike≤0.02T0 (Engel and Singer, 2001) что составляет 0,5 мс для моделирования модели с фазовыми осцилляторами MS и 0,2932 мс для модели с классическими нейронами HH.
Синхронное срабатывание внешних осцилляторов зависит не только от синаптических весов и времени задержки, но также от начальной фазы трех осцилляторов.Следовательно, мы должны учитывать надежность сходимости к синхронному срабатыванию для изменений начальной относительной фазы нейронных осцилляторов. Поэтому мы определяем « качество синхронизации » (SQ) как долю количества начальных комбинаций фаз, которая приводит к стабильному синхронному срабатыванию внешних генераторов. SQ имеет значение от 0 до 100%, где 100% означает, что внешние осцилляторы всегда будут сходиться к синхронному всплеску в течение периода моделирования, независимо от их начальных фаз.Это обеспечивает измерение области притяжения начальных фаз для достижения синхронизации внешних осцилляторов. Чтобы определить SQ, мы повторяем наши модели 35 3 = 42 875 раз со случайно выбранными начальными фазами.
Чтобы исследовать влияние различных параметров окна обучения STDP, мы хотим получить одно значение для SQ, а не одно значение для каждой комбинации синаптических весов и задержки проводимости. Для этого мы рассматриваем различные синаптические веса в 100 равномерно распределенных шагах в диапазоне от 0.01–0,21 и задержки проводимости на 100 равномерно расположенных ступенях в диапазоне от 0,01 до 0,49. Затем мы усредняем SQ по этим 10 000 пар, чтобы получить «средний SQ» для каждого набора параметров окна обучения. Обратите внимание, что для запуска STDP с 60 сеансами это означает, что мы вычисляем почти 400 миллиардов циклов модели для каждого изменения параметров STDP.
Для некоторых комбинаций синаптических весов, времен задержки и начальных фаз состояние синхронизации без запаздывания достигается быстрее, чем для других комбинаций.Поэтому мы определяем « сходимость » (CP) для сети, чтобы обеспечить синхронизацию внешних осцилляторов без запаздывания. Это вычисляется как CP = SQ · (1 — 〈 n sync 〉 / n sessions ), где 〈 n sync 〉 — среднее количество собственных периодов T 0 необходимо для достижения синхронизации с нулевой задержкой. Если синхронизация с нулевой задержкой не установлена в пределах n sessions = 15 циклов, CP равно 0.Обратите внимание, что 〈 n sync 〉 ≤ n sessions с n sessions = 15 для моделирования в этом исследовании, и что этот показатель умножается на SQ для учета готовности системы для достижения синхронизации с нулевой задержкой.
Наконец, нас интересует не только синхронность внешних генераторов, но и относительная фаза φ r для стабильных режимов, в которых генераторы 1 и 3 не синхронизированы.Относительная фаза между внешними осцилляторами определяется как φ r ≡ (t3, nspike − t1, nspike) / T0 со значением от −1 до 1. Поскольку значения для φ r от −1, 0 и 1 относятся к одному и тому же состоянию, мы сообщаем, что φ r масштабируется в диапазоне от -1/2 до 1/2 путем периодического преобразования [-1, -0,5] в [0, 0,5] и [0,5] , 1] до [−0,5, 0] соответственно.
Результаты
Равные времена задержки и силы связи
На рисунках 2A, C показаны результаты моделирования для SQ и CP, соответственно, в зависимости от задержки проводимости τ и синаптического веса ε для модели MS с мгновенными синапсами, одинаковыми временами задержки (τ 1 = τ 3 = τ) и одинаковой прочности связи (ε 12 = ε 21 = ε 23 = ε 32 = ε).Три сплошные черные линии показывают аналитически рассчитанные границы между различными режимами синхронизации с использованием уравнений фазовой синхронизации, подробности см. В разделе «Режимы синхронизации, полученные из уравнения фазовой синхронизации» в Приложении. Верхняя правая область, обозначенная IV, ограничена линией
.
, где χ b определено в уравнении. 7. Для подробного вывода см. Обсуждение ниже уравнения. A12 в Приложении. Наше моделирование показывает, что в области IV синхронизация с нулевым запаздыванием происходит в основном, когда релейный осциллятор дает импульс сразу после поступления синаптического ввода от внешних нейронов, но внешние нейроны не делают этого после ввода от ретрансляционного нейрона, см. Среднюю панель рисунка 2B.Период T IV этого режима «ведомой синхронизации» задается уравнением. A12 «SS2» в Приложении.
Линия, разделяющая области I и II, имеет вид τ = φ c (ε) / 2. В области I синхронизация с нулевым запаздыванием происходит в основном тогда, когда и реле, и внешние генераторы генерируют импульс сразу после поступления синаптического входа, см. Верхнюю панель на рисунке 2B. Это представляет «DS» с периодом T I для всех нейронов, см. Уравнение. A7 в Приложении. Линия, разделяющая области II и III, равна
.
τ = 1-χb2ε-φcε2βb2ε (14)
, где φ c , χ b и β b , определенные в уравнениях 5 и 7, соответственно.Для подробного вывода см. Обсуждение ниже уравнения. A10 в Приложении. Область II показывает в основном синхронизацию ведомого устройства, как область IV, но с другим периодом T II , см. Уравнение. A12 «SS1» в Приложении. В области III синхронизация с нулевой задержкой происходит в основном, когда внешние генераторы генерируют импульс сразу после поступления синаптического входа, в то время как релейный генератор — нет. Эта «синхронность кардиостимулятора», ср. нижняя панель на рисунке 2B имеет период T III в соответствии с формулой.A10 «PS1» в Приложении.
Рисунок 2A показывает, что SQ изменяется с высокого (область I) на низкий (область II) и обратно до промежуточных значений (область III), когда задержка проводимости уменьшается с 0,5 до 0. Анализ стабильности показывает, что области II и IV показывают плохое SQ. потому что ведомая синхронизация, которая доминирует в этих областях, нестабильна, тогда как ведомая синхронизация и синхронизация кардиостимулятора, которые доминируют в областях I и III, асимптотически стабильны и устойчивы к изменениям в начальных фазах.Большинство комбинаций задержки и синаптического веса дают SQ ниже 50%. На рисунке 2C показано, что задержка и синаптический вес в области I приводят к быстрой сходимости к синхронизации в течение примерно четырех циклов. В других регионах синхронизация с нулевым запаздыванием устанавливается гораздо медленнее или вообще не устанавливается.
На рис. 3А показана гистограмма относительной фазы φ r для режимов стабильного кардиостимулятора-ведомого (φ r ≠ 0) и нестабильной ведомой синхронизации (φ r = 0). с задержкой проводимости τ = 0.25 и синаптический вес ε = 0,1 (параметры в области II, см. Рисунок 2A). Возникают две ненулевые относительные фазы, соответствующие стабильному режиму кардиостимулятор-ведомый, и одна фаза с нулевой задержкой, соответствующая нестабильному режиму синхронизации ведомого. Ненулевые относительные фазы имеют одинаковое абсолютное значение из-за симметрии сети. Примерно для 90% начальных фаз осцилляторов система сходится к двум ненулевым относительным фазам и для 10% к состоянию с синхронизацией с нулевой задержкой. Для других значений задержки и веса в областях II, III и IV гистограммы качественно аналогичны гистограммам, показанным на рисунке 3A, i.е., две ненулевые и одна относительная фаза с нулевым запаздыванием. Таким образом, в общем случае синхронизация с нулевым запаздыванием происходит только для очень ограниченного набора начальных фаз в областях параметров II, III и IV.
Чтобы проиллюстрировать, как отличная от нуля относительная фаза изменяется для различных значений параметров в сети, на рисунке 3B показано абсолютное значение | φ r | как функция задержки проводимости τ и синаптического веса ε. Три черные линии на рисунке 3B указывают границы между областями I, II, III и IV, как на рисунке 2, рассчитанные аналитически с использованием уравнения фазовой синхронизации.Чтобы понять результаты на Рисунке 3B, мы рассматриваем режим «ведомый кардиостимулятор», который соответствует положительной относительной фазе, показанной на Рисунках 3C, D. Вертикальные сплошные линии представляют время всплесков для ε = 0,1 и τ = 0,25, а пунктирные линии соответствуют более сильному весу ε = 0,14 на рисунке 3C и большей задержке τ = 0,35 на рисунке 3D, соответственно. Когда синаптический вес увеличивается на рис. 3C, генераторы 2 и 3 будут всплескивать раньше после ввода от генератора 1, тогда как осциллятор 1 всегда дает всплеск сразу после входа от генератора 2.Следовательно, относительная фаза между генераторами 3 и 1 уменьшается при увеличении силы связи. При более длительных временах задержки на Рисунке 3D синаптические входы от осциллятора 2 поступают позже в осцилляторы 1 и 3, как показано пунктирными стрелками. Входной сигнал вызывает мгновенный всплеск генератора 1, но не так для генератора 3. При более длительном времени задержки генератор 3 будет дальше в своем естественном цикле и, следовательно, он будет всплескиваться раньше после входа. Таким образом, генераторы 1 и 3 будут вспыхивать позже, но их относительная разность фаз уменьшается для более длительных задержек.На левой панели рисунка 3В показана относительная фаза как функция задержки, усредненная по всем значениям синаптического взаимодействия. На нижней панели показана относительная фаза как функция силы связи, усредненная по всем задержкам.
Далее мы изучаем синхронизацию для модели с нейронами HH. На рисунках 4A, E показаны результаты моделирования для модели с нейронами HH для SQ и CP, соответственно, как функция задержки проводимости τ и синаптического веса ε для мгновенных синапсов.Сравнение рисунков 4A, E с теми же результатами для генератора MS на рисунках 2A, C показывает, что модель с нейронами HH дает высокий SQ и большой CP для большего диапазона значений τ и ε, чем нейрон MS.
Рис. 4. Отличная синхронизация для альфа-синапсов с коротким временем нарастания . (Верхняя строка) Качество синхронизации (SQ) и (нижняя строка) скорость сходимости (CP) для модели на основе Ходжкина-Хаксли с мгновенными синапсами (A, E) и альфа-синапсами для различных времен нарастания (B – D, F –H) .Сравнение (A, E) с результатами для нейронов MS (см. Рисунки 2A, C) показывает, что SQ и CP явно улучшаются для нейронов HH. Более того, SQ и CP для коротких времен нарастания альфа-синапсов (B, F) лучше, чем для мгновенных синапсов (A, E) , но уменьшаются при более длительных временах нарастания.
Рисунок 4A также показывает, что идеальный SQ невозможен, когда время задержки меньше, чем приблизительно 0,05 внутреннего периода, что примерно соответствует половине рефрактерного периода нейрона HH.Если временная задержка составляет 0,05 T 0 или меньше, временной интервал от всплеска внешних нейронов и импульсного входа от ретрансляционных нейронов к внешним нейронам меньше или равен рефрактерному периоду. В этом случае вход от ретрансляционного нейрона к внешним нейронам поступает в рефрактерный период, что эффективно снижает силу связи, когда внешние нейроны стремятся синхронизироваться, и тем самым отключает режим DS с нулевой задержкой, когда время задержки мало.
На рисунках 4B – D, F – H показаны SQ и CP, соответственно, как функция задержки проводимости τ и синаптического веса ε для модели нейрона HH с альфа-синапсами разного времени синаптического подъема (слева, посередине и справа). столбцы для τ syn = 1, 2 и 3 мс соответственно).Совершенно неожиданно в контексте результатов на рисунках 4A, E, SQ является высоким для очень малых временных задержек для τ syn = 1 мс (рисунок 4B). Это можно понять из того факта, что альфа-синапс добавляет эффективную задержку, так что импульсный сигнал от ретрансляционного нейрона к внешним нейронам поступает после рефрактерного периода, когда внешние нейроны срабатывают идеально синхронно. Когда время нарастания синапсов увеличивается, диапазон временных задержек и синаптических сил с высоким SQ уменьшается, ср.Рисунки 4B – D. Чтобы понять это, предположим, что синаптические входы от релейного генератора поступают, когда фаза генераторов 1 и 3 составляет φ 1 и φ 1 + Δ, соответственно. Если Δ отличается от нуля, тогда осцилляторы 1 и 3 будут вспыхивать в разное время, если только входной сигнал не будет достаточно сильным, чтобы немедленно инициировать всплеск в обоих осцилляторах. Для большего времени нарастания и той же синаптической силы ε принимается меньше входных данных в единицу времени, поскольку синаптические входные данные распространяются на более длительное время.Следовательно, вход от мгновенного синапса (эквивалент «τ syn = 0») или быстрого альфа-синапса (маленький τ syn ) может более легко синхронизировать внешние осцилляторы, чем медленный альфа-синапс (большой τ syn ).
Высокий SQ возможен для коротких времен задержки (τ <0,05), если время синаптического подъема короткое (Рисунок 4B), но меньше, когда время синаптического подъема увеличивается (Рисунки 4C, D). Это говорит о том, что существует диапазон времен нарастания синапсов, которые благоприятствуют высокому SQ для коротких временных задержек.На рисунке 5 показан SQ как функция времени синаптического нарастания τ syn , оцененная при τ = 0,02 для ε = 1 (красный), 2 (зеленый) и 3 (синий) мСм / см 2 . Идеальный SQ достигается, когда время синаптического подъема умеренно велико, то есть примерно от 0,5 до 1 мс, для большого диапазона сил синаптического взаимодействия. Следовательно, умеренно быстрое время нарастания синапсов способствует синхронизации без запаздывания.
Рис. 5. Оптимальная синхронизация для умеренно быстрого времени нарастания синапсов .Качество синхронизации при τ = 0,02 для трех мощностей синапсов ε = 1 (красный), 2 (зеленый) и 3 (синий) мСм / см 2 в модели с альфа-синапсами и нейронами Ходжкина-Хаксли, показанная как функция от время синаптического нарастания τ син . Почти идеальное качество синхронизации может быть получено, когда время нарастания синапсов умеренно велико, то есть примерно от 0,5 до 1 мс.
STDP упрощает синхронизацию без задержек
Теперь мы исследуем влияние STDP на синхронизацию нейрона МС, начиная с простых мгновенных синапсов.На рисунке 6 показаны SQ и CP с короткой (левый столбец) и длинной адаптацией STDP (правый столбец), то есть после первого и шестидесятого сеанса соответственно. Чтобы упростить сравнение с результатами без STDP на рисунке 2, мы нарисовали те же толстые черные линии на рисунке 6, которые разделяют области с разной динамикой, как на рисунке 2. Обратите внимание, что синаптическая сила ε вдоль горизонтальных осей на рисунке 6 представляет начальный синаптический вес , а не конечные значения после адаптации с помощью STDP.Результаты на рисунках 6A, B показывают, что эффект STDP заключается в постепенном расширении диапазона сил связи, которые вызывают синхронизацию. С STDP слабая связь постепенно увеличивается до большей синаптической силы, которая позволяет синхронное срабатывание, соответствующее DS. Аналогичным образом увеличивается CP, см. Рисунки 6C, D.
Рисунок 6. STDP улучшает синхронизацию на больших расстояниях для мгновенных синапсов и уменьшает долю ненулевых относительных фаз . (A, B) Качество синхронизации после первого и 60-го сеанса соответственно. (C, D) Соответствующая скорость схождения. Для задержек проводимости τ ≥ 0,25 синхронность улучшается за счет увеличения начальных весов ε на STDP. (E) | φ r | как на рисунке 3B, но после 60 учебных занятий. (F) Синаптические веса от внешних генераторов к релейному генератору; (G) синаптические веса от релейного генератора к внешним генераторам.Изменения | φ r | по сравнению с рис. 3В, в значительной степени вызваны увеличением синаптических весов за счет STDP. Для сравнения с результатами без STDP мы показываем сплошные черные линии, разделяющие области с разной динамикой на рисунке 2.
Более высокий SQ и более быстрый CP в области II для больших времен задержки на рисунках 6A – D можно понять следующим образом: увеличивая силу связи, STDP преобразует ведомую синхронизацию, которая является нестабильной и доминирующим режимом синхронизации с нулевой задержкой в области II, в DS, которая асимптотически устойчива.Для ведомой синхронизации STDP увеличивает силу связи между генератором реле и внешним генератором. Острая граница связана с максимальной силой связи ε max = 0,21: преобразование синхронности ведомое устройство в привод может произойти только в том случае, если τ превышает τc + ≡φc (εmax) /2≈0,25. Обратите внимание, что полностью улучшенная область привлекательности для синхронизации с нулевой задержкой достигается только после 60 сеансов с STDP. Это говорит о том, что STDP может способствовать синхронности с нулевой задержкой, но обычно только после многих циклов адаптации веса (здесь до 900 колебаний).
На рисунке 7 показано количество сеансов для STDP, необходимое для получения 100% SQ, если сеть начинается с четырьмя одинаково сильными связями в диапазоне между 0 <ε ≤ 0,21 и временами задержки τc + ≤τ <φc (ε) / 2, то есть, когда STDP изменяет синхронизацию ведомого на DS, как только что обсуждалось. Сплошные черные линии на рисунке 7 разделяют области с разной динамикой, как на рисунке 2 (без STDP). Рисунки 7A, B получены в результате прямого моделирования и аналитических расчетов соответственно.Аналитические результаты получены с использованием уравнений A26 и A27 в Приложении итеративно. Результаты моделирования и анализа хорошо согласуются. Для достижения высокого значения SQ в аналитических расчетах сети требуется немного меньшее количество сеансов, потому что они начинаются из состояния подчиненной синхронизации, тогда как прямое моделирование начинается со случайных начальных фаз и достигает управляемого состояния после достижения сначала подчиненной синхронизации. При меньшей начальной силе связи требуется больше времени для достижения стабильной синхронизации с нулевой задержкой с STDP: 20 циклов (около 0.5 с) или более.
Рисунок 7. Время, необходимое для достижения 100% качества синхронизации с помощью STDP . (A) Количество сеансов для достижения 100% качества синхронизации в соответствии с прямым моделированием; (B) То же согласно аналитическим расчетам для преобразования ведомого в ведомую синхронизацию для соответствующей части φc + ≤τ <φcε ∕ 2 области II. Сплошные черные линии в (A, B) разделяют области с разной динамикой, как показано на рисунке 2.
На рисунке 6E показано абсолютное значение ненулевой относительной фазы | φ r | как функция времени задержки τ и синаптического веса ε после сходимости сети к стабильному состоянию по протоколу STDP. Этот результат следует сравнить со случаем без STDP на рисунке 3B. Обратите внимание, что синаптическая сила ε вдоль горизонтальных осей на рисунке 6 представляет начальный синаптический вес в начале моделирования, который, как предполагается, является одинаково сильным для четырех соединений (см.Рисунок 1A) и будет изменяться во время моделирования с помощью STDP. Средние значения конечных синаптических весов показаны как функция задержки и веса на Рисунке 6F (соединения от внешнего генератора к релейному генератору) и Рисунке 6G (соединения от реле к внешним генераторам) соответственно. После тренировки за 60 занятий значения | φ r | для стабильных состояний сети, показанных на рисунке 6E, значительно уменьшаются в области II, в то время как | φ r | незначительно изменяется в регионах I, III и IV по сравнению со значениями до адаптации синапсов с помощью STDP (рис. 3B).Это в значительной степени вызвано увеличением прочности связи в области II, вызванным STDP, как показано на рисунках 6F, G. Итоговые веса в целом очень похожи в обоих направлениях в регионе II. В области III они различаются, потому что синхронность пейсмекера является доминирующей, что подразумевает разное время пре- и постсинаптического возбуждения для ретрансляционных и внешних нейронов и, следовательно, разные эффекты STDP. Окончательные веса в областях I, II и IV на рисунках 6F, G аналогичны, потому что после многих учебных занятий здесь доминирует DS.В DS поведение реле и внешнего осциллятора одинаково, то есть синаптический вход поступает в фазу 2τ и мгновенно вызывает спайк нейрона. Поскольку все соединения начинаются с одинаковым начальным весом, одинаковая адаптация веса применяется к соединениям от реле к внешним генераторам и наоборот.
Чтобы исследовать устойчивость наших результатов к вариациям значений параметра STDP, мы вернемся к мгновенным синапсам. Мы варьировали амплитуды A + и A — дробной синаптической модификации W , см. Уравнение.9 и фиг. 8A. На рисунках 8B, C показаны SQ и CP, соответственно, для различных значений A + и A — в зависимости от количества учебных занятий. Черные линии на рисунке 8 показывают результаты для окна асимметричного обучения с нашими стандартными параметрами STDP, полученными из данных Bi and Poo (1998), а красные линии показывают результаты для меньшего (0,5 A +, 0 : пунктирная линия) и большие (1,5 A +, 0 : жирная линия) значения амплитуды потенцирования A + .Синие линии соответствуют меньшим (0,5 A -, 0 : пунктирная линия) и большим (1,5 A -, 0 : толстая линия) значениям амплитуды депрессии A — .
Рисунок 8. Эффект от изменения окна обучения STDP . (A) Формы окон обучения для различных амплитуд A + и A — . Черные линии представляют стандартный набор параметров (Bi and Poo, 1998), а красные и синие линии показывают изменение значений потенцирования A + и депрессии A — , соответственно, с коэффициентом 0.5 (пунктирные линии) или 1,5 (толстые линии). (B, C) Зависимость среднего качества синхронизации и скорости сходимости соответственно от количества сеансов обучения. Примерно после 25-40 занятий стандартное окно обучения (черные линии) становится оптимальным.
Когда депрессия преобладает над потенцированием (пунктирные красные и сплошные синие линии), SQ плохой даже после многих сеансов, см. Рис. 8B. Более высокие значения потенцирования по сравнению с депрессией приводят к более быстрой и лучшей синхронизации (пунктирные синие и сплошные красные линии).Однако после примерно 25–40 учебных занятий стандартный набор параметров (Bi and Poo, 1998) дает лучшие результаты, т. Е. Более высокие значения среднего SQ и более быструю сходимость к синхронизации, см. Рисунки 8B, C. Чтобы объяснить это, мы рассмотрим, почему средний SQ в области III становится выше для стандартного набора параметров STDP, чем для наборов параметров с преобладанием потенцирования (пунктирные синие и сплошные красные линии на рисунке 8A). Для других регионов (I, II и IV) оба набора параметров дают аналогичные значения среднего SQ, потому что там система переходит в режим DS после нескольких сеансов обучения.
Сначала мы рассмотрим влияние STDP на силу связи в сети, начиная с начальной силы связи ε и времени задержки τ в области III сразу под линией, разделяющей области II и III. STDP увеличит веса ε до больших значений из-за большей потенциации по сравнению с депрессией. Это перемещает (ε, τ) из области III в область II, где режимы синхронизации без запаздывания «SS1» по формуле. A12 в Приложении и «NDS2» уравнения. А13 в Приложении нестабильны. Следовательно, среднее значение SQ в области III уменьшается, поскольку начальные веса ε будут увеличены до значений, которые соответствуют нестабильным режимам синхронизации с нулевой задержкой в области II.Однако, когда начальные веса и времена задержки находятся дальше от линии, разделяющей области II и III, влияние STDP на веса различно. Чтобы понять это, мы сосредоточимся на синхронизации кардиостимулятора, стабильном режиме синхронизации в области III. Период колебаний для синхронизации кардиостимулятора в области III становится больше, когда веса ε становятся меньше, поскольку увеличивается задержка между поступлением импульса импульса и возбуждением, ср. формула «PS1» в уравнении. A10 в Приложении. Поскольку временное окно для депрессии намного больше, чем для потенциации, более длительные задержки больше подавляют потенцирование, оставляя депрессию доминирующей.Близко к синхронизации кардиостимулятора, это касается в основном синапсов от внешних генераторов к ретрансляционному нейрону, поскольку внешние нейроны срабатывают быстро после получения входных данных. Ослабление этих синапсов усиливает синхронность кардиостимулятора. В целом, увеличение силы потенцирования сверх стандартного правила приведет к большему сдвигу (ε, τ) в область II без стабильной синхронизации, оставляя меньше (ε, τ), которые обеспечат стабильную синхронизацию кардиостимулятора. Следовательно, SQ и CP в области III в конечном итоге становятся выше для стандартного набора STDP, чем для набора с преобладанием потенцирования; и среднее значение по всем регионам следует этой тенденции, см. рисунки 8B, C.
Результаты для различных постоянных времени потенцирования τ + и депрессии τ — (не показаны) качественно аналогичны результатам для изменения амплитуд A + и A — , т. Е. Большего Значение τ + относительно τ — приводит к более быстрой и лучшей синхронизации, а стандартные значения для τ + и τ — дают лучшие результаты для синхронизации без запаздывания, когда количество обучающих сессий равно большой.Наши результаты устойчивы к уменьшению депрессии (пунктирная синяя линия) или увеличению потенцирования (сплошная красная линия), но не наоборот (пунктирная красная и сплошная синие линии). На рисунке 9 показаны SQ и CP для модели с STDP с нейронами HH с мгновенными синапсами (рисунки 9A, C, соответственно) и с альфа-синапсами (рисунки 9B, D). Сравнение рисунка 9A с рисунком 4A практически не показывает улучшения SQ с помощью STDP. Однако для альфа-синапсов STDP значительно улучшает средний SQ за счет увеличения синаптического взаимодействия ε (сравните рисунки 9B и 4C).
Рис. 9. Пластичность, зависящая от времени всплеска, улучшает синхронизацию на больших расстояниях для модели с HH нейронами . (A, B) Качество синхронизации после 60-го сеанса для мгновенных синапсов и τ syn = 2 мс альфа-синапса соответственно. (C, D) Соответствующая скорость схождения. Для задержек проведения приблизительно τ ≥ 0,1 синхронность улучшается из-за STDP-опосредованного увеличения синаптической силы ε.
Таким образом, условия, которые способствуют длительной синхронизации с нулевой задержкой, следующие. Во-первых, времена задержки относительно собственной частоты T 0 должны быть достаточно большими, т. Е. Более примерно 0,35 (8,75 мс для T 0 = 25 мс) для модели с фазовыми генераторами MS с мгновенным синапс (см. рисунки 2A, C) и 0,15 (2,2 мс для T 0 = 14,66 мс) для модели с нейронами HH с альфа-синапсом (см.Рисунок 4). Более того, альфа-синапсы с коротким временем нарастания синапсов необходимы для синхронизации с нулевой задержкой при коротких временах задержки (см. Рисунок 5). В-третьих, STDP облегчает синхронизацию, но обычно только после многих циклов адаптации веса (см. Рисунки 6–9).
Когда времена задержки от ретрансляционного нейрона до внешних нейронов не идентичны
Теперь исследуем динамику модели на рисунке 1A, когда времена задержки τ 1 и τ 3 различны.Результаты моделирования (не показаны) показывают, что тогда синхронизация с нулевым запаздыванием теряется, что согласуется с данными Fischer et al. (2006) и Vicente et al. (2008). Аналогичные результаты (не показаны) были получены для модели с нейронами HH. Чтобы понять, почему синхронизация с нулевой задержкой исчезает, когда времена задержки разные, мы рассмотрим сеть MS с мгновенными синапсами. Предположим, что генераторы 1 и 3 срабатывают одновременно. Когда осциллятор 2 генерирует потенциал действия, импульсы достигают осцилляторов 1 и 3 после задержек τ 1 и τ 3 соответственно.Когда пики достигают осцилляторов 1 и 3 в фазе, превышающей критическую фазу, осцилляторы 1 и 3 будут пиковыми сразу после прихода пика. Это означает, что генераторы 1 и 3 генерируют всплески с разницей во времени t1, n + 1 spike-t3, n + 1spike = τ1-τ3T0. Это показывает, что синхронизация с нулевым запаздыванием теряется, когда времена задержки τ 1 и τ 3 различны. Качественно аналогичные результаты (не показаны) получены для асимметричной прочности сцепления.
На рисунке 10 показана гистограмма относительной фазы φ r для различных стабильных режимов для синаптического веса ε = 0.1 для пяти пар задержек проводимости: (τ 1 , τ 3 ) = (0,35, 0,25) на рисунке 10A, (0,25, 0,15) на рисунке 10B, (0,25, 0,25) на рисунке 10C, (0,25, 0,35) на рисунке 10D и (0,15, 0,25) на рисунке 10E. На рисунке 10A показаны два пика относительных фаз около -0,19 и -0,14 вместо трех пиков, показанных на рисунке 10C, которые включают один в нуле. Рисунки 10B, D, E также дают два ненулевых пика вместо трех. Рисунки 10A, B являются зеркальными отображениями рисунков 10D, E, соответственно, потому что времена задержки меняются и внешний нейрон с более короткими всплесками времени задержки сначала дает.По сути, симметричные ненулевые пики на рисунке 10C сжимаются в один для асимметричных задержек, а пик с нулевой задержкой смещается к ненулевому значению, которое равно значению пика с нулевой задержкой. Другие комбинации синаптического веса ε и неравных задержек проводимости τ 1 и τ 3 дают качественно аналогичные результаты.
Рис. 10. Влияние неравных задержек на относительную фазу . (A – E) Гистограммы, показывающие долю начальных фаз, которые сходятся к определенной относительной фазе ε = 0.1 для разных пар (τ 1 , τ 3 ) = (0,35, 0,25), (0,25, 0,15), (0,25, 0,25), (0,25, 0,35) и (0,15, 0,25). Когда задержки между внешним осциллятором и ретрансляционным нейроном становятся асимметричными, одна из ненулевых относительных фаз исчезает, а нулевая относительная фаза смещается к ненулевым значениям, что соответствует состоянию, в котором внешний осциллятор с более короткими задержками всплескивает раньше.
Обсуждение
В этом исследовании мы исследовали условия для синхронизации с нулевой задержкой между двумя нейронными осцилляторами, которые взаимодействуют через релейный осциллятор.Главный результат нашего исследования состоит в том, что для модели с нейронами Ходжкина – Хаксли II типа добиться синхронизации легче, чем для нейронов Миролло – Строгаца I типа. Синапсы с коротким временем нарастания (обычно менее 2 мс) более подходят для достижения синхронизации без запаздывания, чем синапсы с более длительным временем нарастания. С STDP сеть приближается к синхронизации с нулевой задержкой с большей скоростью и для большего диапазона синаптических сил и временных задержек, чем без STDP. Однако, когда времена задержки между двумя синхронизирующими генераторами и релейным генератором различны, нулевая фазовая задержка может легко потеряться.
Сеть, используемая в этом исследовании, представляет собой упрощенную модель взаимодействующих популяций нейронов. Это, очевидно, поднимает вопрос, могут ли наши результаты о синхронизации без запаздывания быть искажены упрощениями, присущими нашей модели. В следующих абзацах ниже мы будем утверждать, что это не так. Наш выбор косвенных взаимодействий между осциллирующими популяциями нейронов, т. Е. Через релейный осциллятор, был вдохновлен предыдущими исследованиями, которые показали, что нейронные генераторы с импульсной связью с прямой возбуждающей связью и задержками сигнала в целом не колеблются при нулевой фазовой задержке (van Vreeswijk и другие., 1994; Эрнст и др., 1995, 1998; Knoblauch and Sommer, 2003; Zeitler et al., 2009), если только нейроны не относятся к типу II с двухфазными PRC (Goel and Ermentrout, 2002; Woodman and Canavier, 2011). Тормозящая связь между непосредственно взаимодействующими осцилляторами может вызвать синхронизацию, близкую к нулевой (van Vreeswijk et al., 1994; Zeitler et al., 2009). Однако доминирующая связь между корковыми областями, такими как V1, V2, V4 и FEF, является скорее возбуждающей, чем тормозящей. Эти соображения привели Фишера и др.(2006) и Vicente et al. (2008), чтобы постулировать сетевую модель осцилляторов, взаимодействующих через релейный осциллятор, которая поддерживает синхронизацию с нулевой задержкой. Подкорковые структуры, такие как таламус, являются хорошими физиологическими кандидатами на роль такого посредника (Theyel et al., 2010). В нашем исследовании подробно рассматривается эта модель релейной сети.
Самая упрощенная версия нашей модели предполагает, что осцилляторы, используемые для представления активности популяции нейронов, относятся к типу Миролло – Строгаца. Осциллятор Миролло – Строгаца соответствует классу нейронов I типа (Ижикевич, 2007).Хотя есть доказательства того, что кортикальные пирамидные клетки могут переключаться между типом I и типом II посредством холинергической модуляции (Ermentrout et al., 2001; Jeong and Gutkin, 2007; Prescott et al., 2008; Stiefel et al., 2008, 2009). ), большинство пирамидных клеток в неокортексе, по-видимому, представляют собой нейроны типа I (Reyes and Fetz, 1993a, b; Kawaguchi, 1995; Erisir et al., 1999; Tateno et al., 2004). Наши результаты показывают, что синхронизацию трудно достичь для модели с нейронами МС типа I для слабых и сильных сил синаптических связей, если только задержки не относительно велики.Чтобы оценить этот результат, следует понимать, что литература по этой теме разделена на исследования, предполагающие слабую связь с использованием бесконечно малых кривых фазового отклика, и другие, предполагающие сильную синаптическую связь. Наши результаты согласуются с результатами Ermentrout (1996), который использовал метод возмущений, который эквивалентен предположению о слабой связи, для сетей нейронов типа I с возбуждающей связью. Однако Миролло и Строгац (1990) сообщили, что почти для всех начальных условий сеть с сильно связанными нейронами типа I (без задержек!) Переходит в состояние с синхронным возбуждением.Когда речь идет о задержках, синхронизация с нулевым запаздыванием теряется (Ernst et al., 1995, 1998). Недавно Wang et al. (2012) показали, что синхронизация в сети с сильно связанными генераторами типа I возможна при отсутствии задержек или с задержками, превышающими половину периода сети. Хотя мы не изучали модель с задержками, превышающими 0,5, наши результаты показывают наибольшую синхронность для длительных задержек, что согласуется с результатами Wang et al. (2012).
Замена нейронов Миролло – Строгаца более реалистичными нейронами Ходжкина – Хаксли II типа позволяет использовать более широкий диапазон синаптических сил и временных задержек, совместимых с синхронизацией с нулевой задержкой.Этот результат предполагает функциональную роль изменений нейрональных свойств от типа I к типу II, что согласуется с предположениями Prescott et al. (2008). Однако пока нет экспериментальных данных, которые можно было бы использовать для проверки гипотезы о том, что свойства пирамидных клеток меняются от типа I к типу II, когда возникает синхронность в популяциях нейронов, насколько нам известно. Другая возможность может заключаться в том, что свойства пирамидных клеток не меняются от типа I к типу II, но что активность интернейронов вызывает сильное торможение после активации пирамидных клеток (см. Börgers et al., 2010, для более развернутого описания эффекта торможения). В этом случае ингибирование интернейронами после возбуждения эффективно вызывает двухфазную PRC с фазовыми задержками в начале цикла возбуждения, а фаза продвигается позже в цикле для пары пирамидная клетка / интернейрон, что способствует синхронности как для прямого взаимодействия между двумя пирамидными, так и между ними. клеток, а также для пирамидных клеток, взаимодействующих через ретрансляционный нейрон.
Задержки в сетях взаимодействующих нейронов могут давать множество сложных поведений с множеством бифуркаций и богатой фазовой диаграммой, которая включает колебательные удары, бегущие волны, качающиеся волны, стоячие волны, возникающие через бифуркацию удвоения периода, апериодические режимы и т. Д. режимы мультистабильности (Roxin et al., 2005). Синхронный запуск — лишь один из этих режимов, который возможен только для ограниченного диапазона параметров модели. Свойство нейронов, которое в значительной степени способствует синхронности, состоит в том, что кривая фазового отклика нейронов является двухфазной с фазовыми задержками в начале цикла активации и фазой прогрессирования позже в цикле, как для нейронов Ходжкина-Хаксли типа II. Это касается как слабосвязанных осцилляторов (см., Например, Hansel, Mato, 1993; Hansel et al., 1993a, b), так и сильносвязанных (Bressloff, Coombes, 2000; Ижикевич, 2007).Их результаты согласуются с результатами нашего исследования, которые показывают, что модель с нейронами Ходжкина-Хаксли II типа легче приводит к синхронизации с нулевым запаздыванием, чем с нейронами МС типа I.
Другое предположение этого исследования, которое требует дальнейшего обсуждения, состоит в том, что все осцилляторы в модели имеют идентичные внутренние свойства с одинаковым периодом колебаний. Если внутренние периоды внешних осцилляторов различаются, синхронизация с нулевым запаздыванием может быть потеряна. Будет ли потеряна синхронность, зависит от типа нейрона.Если синаптический вход для внешних нейронов, которые имеют разные собственные частоты, сбрасывает их периоды колебаний на одно и то же значение, легко достигается синхронизация с нулевым запаздыванием. Синхронизация нелинейных осцилляторов с различными колебательными свойствами возможна, если взаимодействия между осцилляторами (синаптические силы в нашем исследовании) достаточно сильны (Пиковский и др., 2001). Особым условием является ситуация, когда собственный период релейного генератора отличается от периода внешних генераторов.В этом нет ничего необычного, если релейные осцилляторы являются таламическими клетками, а внешние осцилляторы — кортикальными клетками. В этом случае свойства синхронизации меняются количественно, но не качественно. Эти результаты были подтверждены моделированием (не показаны), но их можно понять из следующего: если мы сделаем период релейного осциллятора отличным от периода внешних осцилляторов, комбинации синаптической силы и задержки, при которых входной сигнал может вызвать всплески сразу после прибытие изменяется незначительно с корректировкой периода.Следовательно, границы областей с управляемой, пейсмекерной и подчиненной синхронизацией будут изменяться количественно, но не качественно, если различия в периоде не станут слишком большими.
Если периоды двух внешних осцилляторов отличаются друг от друга и если входной сигнал от релейного осциллятора не делает периоды внешних осцилляторов одинаковыми, то вход от релейного осциллятора во внешние нейроны будет вызывать всплески в разное время. В этом случае импульсный сигнал от внешних генераторов к релейному нейрону также поступает в разное время.Это по сути эквивалентно ситуации с разными временами задержки, которую мы изучали (см. Когда времена задержки от ретрансляционного нейрона до внешних нейронов не идентичны), где мы показали, что синхронизация с нулевой задержкой легко теряется, если времена задержки становятся разные (см. также рисунок 10). Следовательно, сила синаптической связи должна быть достаточно сильной, чтобы гарантировать синхронизацию с нулевой задержкой, когда периоды колебаний внешних осцилляторов различаются.
В нашем исследовании мы ввели «SQ» как меру устойчивости синхронности к изменениям начальных фаз осцилляторов.SQ использовался вместе с «CP» для оценки синхронизма с нулевой задержкой между двумя внешними генераторами в нашей релейной сети. Временной интервал для «синхронности» был выбран как совпадение пиков в пределах 0,5 мс (Engel and Singer, 2001), что в экспериментальных условиях достаточно долго, чтобы учесть типичный шум на временах пиков, но достаточно короткое, чтобы говорить о «нулевой задержке». . » Увеличение временного интервала до 1 мс качественно не повлияло на результаты, хотя количественно наблюдались незначительные отличия.
В согласии с Knoblauch and Sommer (2003), мы обнаружили, что если STDP адаптирует синаптическую связь, состояние сети легче сходится к стабильному состоянию с синхронизацией с нулевым запаздыванием (см. Рисунки 6 и 9). Однако адаптация синапсов с помощью STDP часто занимала довольно много времени [в целом более 500 циклов (один сеанс соответствует 60 циклам), см. Рисунок 7], что означает, что STDP не всегда может играть доминирующую роль для быстрого развития синхронизация с нулевой задержкой. Vicente et al.(2008) сообщили, что механизм синхронизации основан на способности возбуждающего постсинаптического потенциала согласованно изменять латентность активации постсинаптического нейрона. Мы согласны с этим выводом, но наши результаты показывают, что для механизма STDP может потребоваться слишком много времени (значительно больше, чем наблюдаемый временной диапазон 200–250 мс для визуального восприятия, см. Rodriguez et al. (1999)), чтобы сгенерировать нулевое значение. -задержка синхронизации колебаний в гамма-диапазоне частот.
В целом, наши результаты демонстрируют, что гамма-колебания в различных областях коры головного мозга могут быть синхронизированы с нулевым запаздыванием в сетевой модели, в которой нейронные осцилляторы связаны через релейный осциллятор, что согласуется с предыдущими исследованиями (Fischer et al., 2006; Vicente et al., 2008). Кроме того, мы показываем, что STDP расширяет диапазон значений параметров, что обеспечивает синхронизацию с нулевой задержкой.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Этот проект частично финансировался Нидерландской организацией научных исследований (NWO 051.02.050).
Список литературы
Bi, G.-Q., and Poo, M.-M. (1998). Синаптические модификации в культивируемых нейронах гиппокампа: зависимость от времени спайков, синаптической силы и типа постсинаптических клеток. J. Neurosci. 18, 10464–10472.
Pubmed Реферат | Pubmed Полный текст
Bressloff, P.C., and Coombes, S. (1998). Десинхронизация, синхронизация мод и всплеск в сильно связанных генераторах интегрирования и запуска. Phys.Rev. Lett. 81, 2168.
CrossRef Полный текст
Кастело-Бранко, М., Нойеншвандер, С., и Зингер, В. (1998). Синхронизация зрительных ответов между корой, латеральным коленчатым ядром и сетчаткой у кошки под наркозом. J. Neurosci. 18, 6395–6410.
Pubmed Реферат | Pubmed Полный текст
Энгель, А. К., Кониг, П., Крейтер, А. К., Шиллен, Т. Б., и Сингер, В. (1992). Временное кодирование в зрительной коре — новые перспективы интеграции в нервную систему. Trends Neurosci. 15, 218–226.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Эрисир А., Лау Д., Руди Б. и Леонард К. С. (1999). Функция определенных K + каналов в устойчивом высокочастотном возбуждении быстрых всплесков неокортикальных интернейронов. J. Neurophysiol. 82, 2476–2489.
Pubmed Реферат | Pubmed Полный текст
Эрментроут Б., Паскаль М. и Гуткин Б. (2001). Влияние адаптации частоты всплесков и отрицательной обратной связи на синхронизацию нейронных осцилляторов. Neural Comput. 13, 1285–1310.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Эрнст У., Павелзик К. и Гейзель Т. (1998). Мультистабильная синхронизация биологических осцилляторов, вызванная задержкой. Phys. Ред. E 57, 2150–2162.
CrossRef Полный текст
Фишер И., Висенте Р., Булду Дж. М., Пейл М., Мирассо К. Р., Торрент М. К. и Гарсия-Охалво Дж. (2006). Синхронизация на большие расстояния с нулевой задержкой посредством динамической ретрансляции. Phys. Rev. Lett. 97, 123901.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Фрайен А., Экхорн Р., Бауэр Р., Вельберн Т. и Кер Х. (1994). Специфические для стимула быстрые колебания в нулевой фазе между визуальными областями V1 и V2 бодрствующей обезьяны. Neuroreport 5, 2273–2277.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Froemke, R.C., Tsay, I.A., Raad, M., Лонг, Дж. Д., Дэн, Ю. (2006). Вклад отдельных спайков в долговременную синаптическую модификацию, вызванную взрывом. J. Neurophysiol. 95, 1620–1629.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Гоэль, П., и Эрментроут, Б. (2002). Синхронность, стабильность и схемы срабатывания в генераторах с импульсной связью. Physica D 163, 191–216.
CrossRef Полный текст
Goldbeter, A. (1996). Биохимические колебания и клеточные ритмы: молекулярные основы периодического и хаотического поведения .Кембридж: Издательство Кембриджского университета.
Грей, К. М., Кониг, П., Энгель, А. К., и Сингер, В. (1989). Колебательные реакции зрительной коры головного мозга кошки демонстрируют межколоночную синхронизацию, которая отражает глобальные свойства стимула. Природа 338, 334–337.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Гросс Дж., Шмитц Ф., Шницлер И., Кесслер К., Шапиро К., Хоммель Б. и Шницлер А. (2004). Модуляция дальнодействующей нейронной синхронности отражает временные ограничения зрительного внимания у людей. Proc. Natl. Акад. Sci. США 101, 13050–13055.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Hansel, D., и Mato, G. (1993). Паттерны синхронности в гетерогенной нейронной сети Ходжкина-Хаксли со слабой связью. Physica A 200, 662–669.
CrossRef Полный текст
Hansel, D., Mato, G., and Meunier, C. (1993a). Кластеризация и медленное переключение в глобально связанных фазовых осцилляторах. Phys. Ред. E 48, 3470–3477.
CrossRef Полный текст
Hansel, D., Mato, G., and Meunier, C. (1993b). Фазовая динамика для слабосвязанных нейронов Ходжкина-Хаксли. еврофиз. Lett. 23, 367.
CrossRef Полный текст
Хебб, Д. О. (1949). Организация поведения: нейропсихологическая теория . Нью-Йорк: Вили.
Хеннекен, Г., Герстнер, В., и Пфистер, Дж. П. (2010).STDP в адаптивных нейронах обеспечивает передачу информации, близкую к оптимальной. Фронт. Comput. Neurosci. 4: 143. DOI: 10.3389 / fncom.2010.00143
CrossRef Полный текст
Ходжкин А. Л. и Хаксли А. Ф. (1952). Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве. J. Physiol. (Лондон) 117, 500–544.
Pubmed Реферат | Pubmed Полный текст
Ижикевич, Э.М. (2007). Динамические системы в неврологии: геометрия возбудимости и взрыва . Кембридж, Массачусетс: MIT Press.
Кавагути Ю. (1995). Физиологические подгруппы непирамидных клеток со специфическими морфологическими характеристиками в слое Ii / Iii лобной коры головного мозга крыс. J. Neurosci. 15, 2638–2655.
Pubmed Реферат | Pubmed Полный текст
Кноблаух А. и Соммер Ф. Т. (2003). Синаптическая пластичность, задержки проводимости и межплощадочные фазовые отношения спайковой активности в модели взаимно связанных областей. Нейрокомпьютеры 52–54, 301–306.
CrossRef Полный текст
Кох, К., Сегев, И. (1998). Методы нейронного моделирования: от ионов к сетям . Кембридж, Массачусетс: MIT Press.
Ли С., Сен К. и Копелл Н. (2009). Корковые гамма-ритмы модулируют опосредованную NMDAR пластичность, зависящую от времени спайков, в биофизической модели. PLoS Comput. Биол. 5, e1000602. DOI: 10.1371 / journal.pcbi.1000602
CrossRef Полный текст
Миролло, Р.Э. и Строгац С. Х. (1990). Синхронизация биологических осцилляторов с импульсной связью. SIAM J. Appl. Математика. 50, 1645–1662.
CrossRef Полный текст
Песаран Б., Пезарис Дж. С., Сахани М., Митра П. П. и Андерсен Р. А. (2002). Временная структура нейрональной активности во время рабочей памяти в теменной коре макака. Нац. Neurosci. 5, 805–811.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Пиковский, А., Розенблюм, М., и Куртс, Дж. (2001). Синхронизация: универсальная концепция нелинейных наук . Кембридж: Издательство Кембриджского университета.
Прескотт, С. А., Ратте, С., Де Конинк, Ю., и Сейновски, Т. Дж. (2008). Пирамидные нейроны переключаются с интеграторов in vitro на резонаторы в условиях, подобных in vivo. J. Neurophysiol. 100, 3030–3042.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Рейес, А.Д., и Фец, Э. Э. (1993a). Влияние переходных деполяризующих потенциалов на скорость возбуждения нейронов неокортекса кошек. J. Neurophysiol. 69, 1673–1683.
Рейес А. Д. и Фетц Э. Э. (1993b). Два режима сокращения межспайкового интервала за счет кратковременных переходных деполяризаций в нейронах неокортекса кошек. J. Neurophysiol. 69, 1661–1672.
Родригес, Э., Джордж, Н., Лашо, Дж. П., Мартинери, Дж., Рено, Б., и Варела, Ф.Дж. (1999). Тень восприятия: дальняя синхронизация мозговой активности человека. Природа 397, 430–433.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Роксин А., Брунель Н. и Гензель Д. (2005). Роль задержек в формировании пространственно-временной динамики нейрональной активности в больших сетях. Phys. Rev. Lett. 94, 1–4.
CrossRef Полный текст
Штифель, К.М., Гуткин, Б.С., Сейновски Т. Дж. (2008). Холинергическая нейромодуляция изменяет форму и тип кривой фазового ответа в корковых пирамидных нейронах. PLoS ONE 3, e3947. DOI: 10.1371 / journal.pone.0003947
CrossRef Полный текст
Штифель, К. М., Гуткин, Б. С., Сейновски, Т. Дж. (2009). Влияние холинергической нейромодуляции на кривые фазового ответа нейронов смоделированных корковых нейронов. J. Comput. Neurosci. 26, 289–301.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Татено, Т., Харш А. и Робинсон Х. П. С. (2004). Пороговые отношения частота-ток нейронов в соматосенсорной коре крыс: динамика типа 1 и типа 2. J. Neurophysiol. 92, 2283–2294.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Цубо Ю., Такада М., Рейес А. Д. и Фукаи Т. (2007). Слойные и частотные зависимости свойств фазового отклика пирамидных нейронов моторной коры головного мозга крыс. евро. J. Neurosci. 25, 3429–3441.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
ван Россум, М. К. У., Би, Г. К., и Турриджиано, Г. Г. (2000). Стабильное обучение Хебба благодаря пластичности, зависящей от времени всплеска. J. Neurosci. 20, 8812–8821.
Pubmed Реферат | Pubmed Полный текст
Висенте Р., Голло Л. Л., Мирассо К. Р., Фишер И. и Пипа Г. (2008). Динамическая ретрансляция может дать нейронную синхронизацию с нулевым запаздыванием, несмотря на длительную задержку проведения. Proc. Natl. Акад. Sci. США 105, 17157–17162.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Ван С., Чандрасекаран Л., Фернандес Ф. Р., Уайт Дж. А. и Канавье К. С. (2012). Кратковременные задержки проводимости вызывают торможение, а не возбуждение, что способствует синхронности в гибридных нейронных сетях энторинальной коры. PLoS Comput. Биол. 8, e1002306. DOI: 10.1371 / journal.pcbi.1002306
CrossRef Полный текст
Вудман, М.М., и Канавье, К. С. (2011). Влияние задержек проводимости на наличие и стабильность однофазной синхронизации между двумя генераторами с импульсной связью. J. Comput. Neurosci. 31, 401–418.
Pubmed Реферат | Pubmed Полный текст | CrossRef Полный текст
Приложение
Подробный анализ фазовой синхронизации и стабильности
Приведены аналитические выводы различных режимов синхронности и их устойчивости. Обзор этих результатов представлен на рисунке A1.
Режимы синхронизации, выведенные из уравнения фазовой синхронизации
Чтобы исследовать существование синхронизма с нулевым запаздыванием как функции τ и ε, мы выведем уравнение синхронизации 1: 1 для синхронизированных фаз осцилляторов, ср. Рисунок 1B. Срабатывание ретрансляционного нейрона t2, n-1spike выбрано в качестве эталонного времени, то есть t2, n-1spike = 0. Для синхронизации с нулевым запаздыванием существует некоторое значение þeta ∈ [0, 1) такое, что времена срабатывания t1, n-1spike и t3, n-1spike обоих нейронов 1 и 3 равны θ T , а t1, nspike и t3, nspike равны θ T + T , при T период колебаний в сети.Пики от внешних генераторов поступают в генератор реле в фазе τ + θ T / T 0 , если τ ≤ (1 — θ) T / T 0 , или при τ — (1 — θ) T / T 0 , если τ> (1 — θ) T / T 0 . Таким образом, новый период внутреннего осциллятора 2 равен
.
T = T0-T0Δτ + θTT02ε для τ≤1 — θTT0T0-T0Δτ-1-θTT02ε для τ> 1 — θTT0, (A1)
, где Δφ определено в уравнениях 6 и 7 основного текста, повторенных здесь для удобства:
Δφiφiεij = χbεij + βbεijφifor0≤φi <φc1-φiforφc≤φi <1, (A2) χbx≡βbxβb1, βbx≡ebx-1.(A3)
Рисунок A1. Области синхронизации в плоскости параметров времени задержки и силы связи . Различные комбинации возможных режимов синхронизации делят плоскость параметров времени задержки τ и синаптического веса ε на десять отдельных областей. Они показаны разделенными черными линиями, а соответствующие режимы синхронизации обозначены символами, относящимися к результатам, перечисленным в Приложении: управляемая синхронизация — уравнение. A7 «DS» в Приложении; синхронизация кардиостимулятора — Ур.A10 «PS1» и «PS2» в Приложении; ведомая синхронизация — ур. A12 «SS1» и «SS2» в Приложении; и синхронность без привода — ур. A13 «NDS1», «NDS2» и «NDS3» в Приложении.
Пик от осциллятора 2 достигнет осцилляторов 1 и 3 в фазе τ + (1 — θ) T / T 0 , если τ ≤ θ T / T 0 , или τ — θ T / T 0 , если τ> θ T / T 0 . Таким образом, новый период внешних осцилляторов 1 и 3 равен
.
T = T0-T0Δφτ + 1-θTT0ε для τ≤θTT0T0-T0Δφτ-θTT0ε для τ> θTT0.(A4)
Уравнения A1 и A4 представляют собой уравнения синхронизации 1: 1, которые определяют соотношение между синаптическим весом ε, задержкой проводимости τ и новым периодом осцилляторов T .
Используя уравнения A1 и A4, мы получим четыре режима синхронизации: управляемая, кардиостимулятор, подчиненная и неуправляемая синхронизация. В управляемой синхронности спайки от внешних нейронов немедленно инициируют спайк ретрансляционного нейрона, и наоборот, ср. вверху рисунка 2B. При синхронизации с кардиостимулятором приход импульса от релейного генератора к внешним генераторам немедленно вызывает всплеск, но не наоборот, ср.внизу рисунка 2B. Когда релейный нейрон дает импульс сразу после импульса от внешних нейронов, но не наоборот, мы называем это подчиненной синхронностью, ср. середина рисунка 2В. Наконец, неуправляемая синхронизация возникает, когда ни релейный нейрон, ни внешние нейроны не запускают импульс сразу после ввода.
Сначала рассмотрим управляемую синхронизацию. Чтобы все входные пики вызывали пики в принимающих генераторах, мы должны иметь следующее: для внутреннего генератора φ c (2ε) ≤ τ + θ T / T 0 , если τ ≤ (1 — θ) T / T 0 и φ c (2ε) ≤ τ — (1 — θ) T / T 0 если τ> (1 — θ) T / T 0 ; а для внешних осцилляторов φ c (ε) ≤ τ + (1 — θ) T / T 0 , если τ ≤ θ T / T 0 , и φ c (ε) ≤ τ — θ T / T 0 , если τ> θ T / T 0 .Используя уравнения A1, A2 и A4, мы можем затем переписать новый период внутреннего осциллятора как
.
T = τT0 + θT для τ≤1-θTT0 и φc2ε≤τ + θTT0τT0-1-θT для τ> 1-θTT0 и φc2ε≤τ-1-θTT0, (A5)
и новый период внешних осцилляторов как
T = τT0 + 1-θT для τ≤θTT0 и φcε≤τ + 1-θTT0τT0-θT для τ> θTT0 и φcε≤τ-θTT0. (A6)
Теперь мы можем решить для θ и T , используя по одной части уравнений A5 и A6 и комбинируя их при условии, что новые периоды T внутреннего и внешнего осцилляторов, соответственно, должны быть идентичны для достижения синхронизации. .Это дает четыре возможных комбинации:
θ, TT0 = 12,2τ для φcε≤2τ и φc2ε≤2τDS0, τ для φcε≤τ и φc2ε≤τ1, τ для φcε≤τ и φc2ε≤τ12,23τ для φcε≤23τ и φc2ε≤23τ. (A7)
Для биологически реалистичных условий τ ∈ (0, 0,5) и ε ∈ (0, 0,21) и нашего выбора b = 3, только режим управляемой синхронизации, обозначенный как «DS», оказывается действительным. Динамика срабатывания «DS» проиллюстрирована в верхней части рисунка 2B. В остальных случаях условия φ c не выполняются, и поэтому эти решения отклоняются.Более того, третье решение также имеет значение θ вне диапазона для фазовой синхронизации 1: 1. Ниже мы аналогичным образом определим допустимые режимы других решений. Поскольку φ c (2ε) ≤ φ c (ε), φ c (ε) ≤ 2τ подразумевает φ c (2ε) ≤ 2τ, а φ c (ε) ≤ 2τ достаточно. Это ограничение делит пространство параметров ε и τ на две области: управляемая синхронизация возможна в области, где φ c (ε) ≤ 2τ, но не в области, где φ c (ε)> 2τ.Эти две области разделены линией φ c (ε) = 2τ, показанной линией, разделяющей области I и II на рисунках 2A, C.
Во-вторых, мы исследуем синхронизацию кардиостимулятора. Для синхронизации кардиостимулятора только внешние осцилляторы срабатывают непосредственно при входе, но не внутренний. Таким образом, для внутреннего осциллятора мы должны иметь φ c (2ε)> τ + θ T / T 0 , если τ ≤ (1 — θ) T / T 0 и φ c (2ε)> τ — (1 — θ) T / T 0 , если τ> (1 — θ) T / T 0 .Для внешних осцилляторов мы должны иметь φ c (ε) ≤ τ + (1 — θ) T / T 0 , если τ ≤ θ T / T 0 , и φ c (ε) ≤ τ — θ T / T 0 , если τ> θ T / T 0 . Используя уравнение. A2 в Приложении, мы можем переписать новый период внутреннего осциллятора, заданный формулой. A1 в Приложении как
T = T0γb2ε-θTβb2ε для τ≤1-θTT0 и φc2ε> τ + θTT0T0γb2ε + 1-θTβb2ε для τ> 1-θTT0 и φc2ε> τ-1-θTT0, (A8) γbx≡1-χbx, (A8) γbx≡1-χbx,
, где новый период внешних осцилляторов задается формулой.A6 в Приложении. Решая для θ и T , как и раньше, мы находим следующие четыре возможности:
θ, TT0 = τT0T, γb2ε-βb2ετ для φcε≤TT0 и φc2ε> 2τPS1τT0T-1, γb2ε-βb2ετ1-βb2ε для φcε≤TT0 и φc2ε> 2τ-TT0τT0T, γb2ε-cb2ε-TT0-β2ε-βcb2τ0-φτ2> φτ0-βτ2> , γb2ε-βb2ετ1-2βb2ε для φcε≤TT0 и φc2ε> 2τ-2TT0. (A10)
Два допустимых режима для синхронизации кардиостимулятора с учетом наших ограничений обозначены «PS1» и «PS2» в уравнении. A10 в Приложении соответственно. В пределах нашего интересующего диапазона значений ε и τ можно численно проверить синхронность кардиостимулятора «PS1» и «PS2», что φ c (ε) ≤ T / T 0 подразумевает φ c (2ε)> 2τ и φ c (2ε)> 2τ — T / T 0 соответственно.Следовательно, требуется только ограничение φ c (ε) ≤ T / T 0 . Синхронизация кардиостимулятора «PS1» возможна в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | φ c (ε) ≤ T / T 0 } ; в то время как «PS2» возможен в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | φ c (ε) ≤ T / T 0 и ( 1 — θ) T / T 0 <τ}, где (1 - θ) T / T 0 <τ относится к условию, приведенному в уравнении.A1 в Приложении. Равенство φ c (ε) = T / T 0 «PS1» дает линию, разделяющую области II и III на рисунках 2A, C. Динамика возбуждения для синхронизации кардиостимулятора «PS1» проиллюстрирована на рисунке 2B.
В-третьих, при синхронизации ведомого только внутренний генератор генерирует пики на входе, т.е. в случае внутреннего генератора мы должны иметь φ c (2ε) ≤ τ + θ T / T 0 , если τ ≤ (1 — θ) T / T 0 и φ c (2ε) ≤ τ — (1 — θ) T / T 0 если τ> ( 1 — θ) T / T 0 .Для внешних осцилляторов мы должны иметь φ c (ε)> τ + (1 — θ) T / T 0 , если τ ≤ θ T / T 0 , и φ c (ε)> τ — θ T / T 0 , если τ> θ T / T 0 . Новый период внутреннего осциллятора определяется формулой. A5 в Приложении и из уравнений A2 и A4 мы получаем следующее выражение для нового периода внешнего осциллятора
T = T0γbε-1-θTβbε для τ≤θTT0 и φcε> τ + 1-θTT0T0γbε + θTβbε для τ> θTT0 и φcε> τ-θTT0.(A11)
Итак, четыре комбинации:
θ, TT0 = 1-τT0T, γbε-βbετ для φcε> 2τ и φc2ε≤TT0SS11-τT0T, γbε-βbετ1-βbε для φcε> 2τ-TT0 и φc2ε≤TT0SS22-τT0T, γbε-βεbετ0-β для φτ1-β ≤TT02-τT0T, γbε-βbετ1-2βbε для φcε> 2τ-2TT0 и φc2ε≤TT0. (A12)
Два допустимых режима синхронизации ведомого устройства будут называться «SS1» и «SS2» соответственно. В пределах нашего интересующего диапазона значений ε и τ можно численно проверить для режима синхронизации ведомого устройства «SS1», что φ c (ε)> 2τ подразумевает φ c (2ε) ≤ T / Т 0 ; тогда как ограничения для «SS2» всегда выполняются в наших диапазонах для ε и τ.Следовательно, синхронизация ведомого устройства «SS1», динамика срабатывания которого проиллюстрирована на рисунке 2B, возможна в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | φ c (ε )> 2τ}; в то время как «SS2» возможен в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | τ> θ T / T 0 }, где τ> θ T / T 0 относится к условию, приведенному в формуле. A4 в Приложении. Равенство τ = θ T / T 0 «SS2» дает линию, разделяющую области I и IV на рисунках 2A, C.
Наконец, для синхронизма без привода ни один из осцилляторов не срабатывает сразу после получения пика. Это означает, что для внутреннего осциллятора φ c (2ε)> τ + θ T / T 0 , если τ ≤ (1 — θ) T / T 0 , и φ c (2ε)> τ — (1 — θ) T / T 0 , если τ> (1 — θ) T / T 0 . Для внешних осцилляторов φ c (ε)> τ + (1 — θ) T / T 0 , если τ ≤ θ T / T 0 и φ c (ε)> τ — θ T / T 0 , если τ> θ T / T 0 .Затем новый период задается уравнениями A8 и A11 для внутреннего и внешнего осцилляторов соответственно. Получающиеся комбинации:
θ, TT0 = ρ ++ — 0ρ0 + 0 +, ρ0 + 0 + ζ + для φcε> τ-ρ + 0 — ζ + и φc2ε> τ + ρ ++ — 0ζ + NDS1ρ + 0-0ρ0 + 0 + , ρ0 + 0 + ζ0 для φcε> τ-ρ + 0-0ζ0 и φc2ε> τ + ρ + 0-0ζ0ρ ++ — + ρ0 + 0 +, ρ0 + 0 + ζ0 для φcε> τ-ρ + 0-0ζ0 и φc2ε > τ + ρ + 0-0ζ0NDS2ρ + 0- + ρ0 + 0 +, ρ0 + 0 + ζ- для φcε> τ-ρ + 0- + ζ- и φc2ε> τ + ρ + — 0ζ-NDS3 (A13)
с ρ mnop = [ m + n β b (ε)] γ b (2ε) + [ o + p β b ( 2ε)] γ b (ε), где индексы могут принимать значения +1, 0, −1, обозначенные знаками, а также ζ m ≡ β b (ε ) + β b (2ε) + м β b (ε) β b (2ε).Три допустимых режима синхронизации без управления будут называться NDS1, NDS2 и NDS3 соответственно. Из ограничений ε и τ для ведомой синхронизации «NDS1», φ c (ε)> τ — ρ + 0−− / ζ + подразумевает φ c (2ε)> τ + ρ ++ — 0 / ζ + . Для ведомой синхронизации «NDS2» φ c (ε)> τ — ρ + 0-0 / ζ 0 подразумевает φ c (2ε)> τ + ρ + 0− 0 / ζ 0 .Но ограничения «NDS3» автоматически выполняются в нашем диапазоне значений ε и τ. Следовательно, синхронизация ведомого «NDS1» возможна в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | φ c (ε)> τ — ρ + 0−− / ζ + }; в то время как «NDS2» возможен в области {(ε, τ) ∈ [0, 0,21] × [0, 0,5] | φ c (ε)> τ — ρ + 0−0 / ζ 0 и τ> (1 — θ) T / T 0 } и «NDS3» в области {(ε, τ) ∈ [0, 0.21] × [0, 0,5] | τ> (1 — θ) T / T 0 }, где τ> (1 — θ) T / T 0 относится к условию приведенный в формуле. A1 в Приложении.
На основе различных комбинаций режимов синхронизации DS из уравнения. A7 в Приложении, PS1 и PS2 из уравнения. A10 в Приложении, SS1 и SS2 из уравнения. A12 в Приложении и NDS1, NDS2 и NDS3 из уравнения. A13 в Приложении, мы можем разделить плоскость параметров временной задержки τ и синаптического веса ε на десять областей, см. Рисунок A1.Таким образом, области в пространстве параметров ε и τ, в которых возможны режимы, представлены как
{(ε, τ) ∈ [0,0.21] × [0,0.5] | φc (ε) ≤2τ} для DS, {(ε, τ) ∈ [0,0.21] × [0,0.5] | φc ( ε) ≤T / T0} для PS1, {(ε, τ) ∈ [0,0.21] × [0,0.5] | φc (ε) ≤T / T0 и (1 − θ) T / T0 <τ} для PS2, {(ε, τ) ∈ [0,0.21] × [0,0.5] | φc (ε)> 2τ} для SS1, {(ε, τ) ∈ [0,0.21] × [0,0.5] | τ> θT / T0} для SS2, {(ε, τ) ∈ [0,0.21] × [0,0.5] | φc (ε)> τ − ρ + 0 −− / ζ +} для NDS1, {(ε , τ) ∈ [0,0.21] × [0,0.5] | φc (ε)> τ − ρ + 0−0 / ζ0 и τ> (1 − θ) T / T0} для NDS2, {(ε, τ ) ∈ [0,0.21] × [0,0.5] | τ> (1 − θ) T / T0} для NDS3.(A14)
Анализ устойчивости режимов синхронности
Чтобы исследовать устойчивость управляемой синхронности, мы предполагаем, что фиксированная точка уравнения. A7 «DS» в Приложении страдает от небольших фазовых возмущений (φ 1 , φ 3 ) = (τ + δφ 1 , τ + δφ 1 ) в момент времени t2, n-1 пик. Управляемая синхронизация является асимптотически устойчивой, если существует δ> 0 такое, что фазы внешних осцилляторов будут ближе к τ в следующий момент времени t2 всплеска, nspike для δφ12 + δφ32 <δ.Поскольку φ c (ε) <2τ, мы можем определить δ ≡ 2τ - φ c (ε)> 0, и по этому определению φ c (ε) ≡ 2τ — δ. Всплеск от реле возникает, когда генератор 1 имеет фазу 2τ — δ <φ 1 <2τ + δ, что превышает критическую фазу φ c (ε). Таким образом, генератор 1 сразу после ввода будет активировать импульс. Поскольку тот же аргумент применим к осциллятору 3, внешние осцилляторы снова будут синхронно вспыхивать, что доказывает асимптотическую устойчивость для малых возмущений.Аналогичные аргументы можно привести, чтобы показать, что синхронность кардиостимулятора уравнения. Пункты A10 «PS1» и «PS2» в Приложении асимптотически устойчивы.
Затем мы исследуем стабильность режима синхронизации ведомого Ур. A12 «SS1» в Приложении. Здесь необходимо вычислить собственные значения λ якобиана карты возврата вблизи фиксированной точки фаз внешнего осциллятора (Zeitler et al., 2009). Если все собственные значения находятся внутри единичной окружности (| λ | <1), то неподвижная точка асимптотически устойчива, в противном случае она неустойчива.Предположим, что в момент времени t2, n-1 всплеск, что фазы возмущены от фиксированной точки уравнения. A12 «SS1» в Приложении: (φ 1 , φ 3 ) = (τ + δφ 1 , τ + δφ 3 ). Таким образом, синаптические входы от осцилляторов 1 и 3 будут поступать на осциллятор 2 в несколько разное время. Без ограничения общности мы предполагаем, что синаптический вход от генератора 1 поступает раньше. Этот первый синаптический вход может немедленно вызвать всплеск релейного генератора, если φ c (ε) <τ + θ T / T 0 .Предполагая, что возмущение достаточно мало для решения в уравнении. A12 «SS1» в Приложении остается применимым, мы находим φ c (ε) <τ + θ T / T 0 = 1 — χ b (ε) — 2β b (ε) τ = [1 + β b (ε)] φ c (ε) — 2β b (ε) τ. Для ненулевой связи это эквивалентно 2τ <φ c (ε), что является биологически приемлемым (Tsubo et al., 2007). Поэтому мы предполагаем, что φ c (ε) <τ + θ T / T 0 , и пик от генератора 1 вызовет мгновенный выброс генератора реле, когда он появится. Определите φ̃1 как фазу генератора 1 в это время всплеска реле t2, nspike, тогда, очевидно, φ̃1 = τ, задержка проводимости.
Чтобы найти фазу φ̃3 осциллятора 3, когда пик осциллятора 2 в момент t2, nspike, мы сначала вычисляем предыдущие времена пиковых значений внешних осцилляторов t1, n-1spike и t3, n-1spike.Фаза генератора 1 равна τ + δφ 1 , когда релейный генератор срабатывает в момент t2, n-1 пик .0. После задержки τ T 0 пик от релейного генератора достигает генератора 1, то есть его фазы φ1old = 2τ + δφ1. Если δφ 1 достаточно мало, мы все же можем предположить, что 2τ + δφ 1 <φ c (ε), то есть этот вход от реле не вызовет мгновенный выброс генератора 1. Вместо этого его фаза изменится на φ1new = φ1old + χbε + βbεφ1old, ср.Уравнение A2 в Приложении. После получения пика требуется некоторое время T01-φ1new, пока осциллятор 1 не сработает в момент t1, n-1spike. Следовательно, t1, n-1 spike получается добавлением задержки проводимости τ T 0 между осциллятором 2 и 1 к времени T01-φ1new, что осциллятор 1 все еще должен развиваться перед выбросом. Время всплеска t3, n-1 может быть получено аналогичным образом, и, таким образом, получается:
t1, n-1 острие = T01-χbε-βbετ-1 + βbετ + δφ1, (A15) t3, n-1 острие = T01-χbε-βbετ-1 + βbετ + δφ3. (A16)
Следующий всплеск релейного генератора происходит в t2, nspike = t1, n-1spike + τT0, как объяснено выше.Поскольку φ˜3 = (t2, nspike − t3, n − 1spike) / T0 = τ + (t1, n − 1spike − t3, n − 1spike) / T0, мы находим следующую карту возврата для нашего локального анализа устойчивости
φ̃1 = τ, (A17) φ̃3 = τ-1 + βbεφ1 + 1 + βbεφ3. (A18)
Соответствующая матрица Якоби равна
.
00-1 + βbε1 + βbε. (A19)
Собственные значения этой матрицы равны 0 и 1 + β b (ε)> 1. Следовательно, эта фиксированная точка не является устойчивой. Аналогичным образом можно показать, что уравнение A12 «SS2» в Приложении является нестабильным.
Наконец, мы исследуем устойчивость неуправляемой синхронизации (уравнение). A13 «NDS1» в Приложении. Мы обсудим обратную карту вблизи фиксированной точки φ1 *, φ3 * = 1-θT, 1-θT. В момент времени t2, n-1 пик мы предполагаем небольшое возмущение φ1, φ3 = φ1 * + δφ1, φ3 * + δφ3. Аргументы, использованные для вывода уравнений A15 и A16, справедливы, за исключением того, что возмущенная неподвижная точка равна τ + δφ1 → φ1 * + δφ1 и τ + δφ3 → φ3 * + δφ3 соответственно. Без ограничения общности мы предполагаем, что синаптический вход от осциллятора 1 поступает на осциллятор 2 раньше, чем от осциллятора 3.Таким образом, когда пик осциллятора 1 возникает в момент t1, n-1, импульсный сигнал от осциллятора 1 поступает на осциллятор 2 в фазе t1, n-1 пик / T0 + τ и вызывает изменение фазы осциллятора 2 на χbε + 1 + βbεt1, n -1 острие / T0 + τ. Тогда пик, сгенерированный в момент t3, n-1, пик осциллятором 3 придет, когда осциллятор 2 имеет фазу χbε + 1 + βbεt1, n-1 пик / T0 + τ + t3, n-1 пик-t1, n-1 пик / T0, и это вызывает изменение фазы генератора 2 на
φ2new≡1 + βbεχbε + 1 + βbεt1, n-1 spike / T0 + τ + t3, n-1 spike-t1, n-1 spike / T0 + χbε, (A20) Δt≡1-φ2newT0, (A21)
с выбросом осциллятора 2 после этого дополнительного времени Δ t прошло.Следовательно, фазы внешних осцилляторов в момент времени t2, nspike, когда осциллятор 2 дает всплески, равны
.
φ̃1 = τ + ΔtT0 + t3, n-1 spike-t1, n-1spikeT0, (A22) φ̃3 = τ + ΔtT0. (A23)
Соответствующая матрица Якоби равна
.
1 + βbε1 + βbε1 + βbε1 + βbεβbεβbε1 + βbε21 + βbε2, (A24)
с результирующими собственными значениями
λ1 = 1 + βb (ε), λ2 = 1 + βb (ε) 3. (A25)
Эта фиксированная точка нестабильна, потому что эти собственные значения превышают значение единицы для ε∈ (0, 0,21). Аналогичным образом можно показать, что уравнение.A13 «NDS2» и «NDS3» в Приложении нестабильны.
Влияние STDP на сцепление в ведомой синхронизации
В режиме ведомой синхронизации силы связи между внешними генераторами и релейным генератором остаются неизменными по протоколу STDP, поскольку релейный генератор мгновенно подскакивает при поступлении от внешних генераторов. Как насчет связи генератора реле с внешними генераторами? Скажем, их сила равна ε n — 1 сразу после всплеска внешних осцилляторов в момент t1, n-1spike = t3, n-1spike.Релейный импульс возникает, когда внешние генераторы имеют фазу 2τ, поскольку релейный генератор срабатывает на их фазе τ. Принимая во внимание все предыдущие всплески внешних генераторов в моменты времени t1, lspike, этот новый всплеск реле, приходящий в момент времени t1, n-1spike + 2τT0, изменяет силу связи на
.
ε̃n-1 = εn-1 + εn-1∑l = 0n-1Wt1, lspike-t1, n-1spike + 2τT0 / 60 <εn-1. (A26)
Обратите внимание, что это изменение представляет собой уменьшение прочности сцепления, поскольку t1, lspike
.
εn = ε̃n-1 + ε̃n-1∑k = 0n-1W1-2τT0-T0Δφ2τεn-1 + t1, n-1spike-t1, kspike / 60> ε̃n-1. (A27)
При определенных условиях, см. Основной текст, это приводит к тому, что STDP превращает ведомую синхронизацию в управляемую синхронизацию, и время перехода может быть определено путем численного повторения формул для ε˜n − 1 и ε n .
.

 Это может ввести в заблуждение обслуживающий персонал, который будет проводить ремонт или ревизию электропроводки
Это может ввести в заблуждение обслуживающий персонал, который будет проводить ремонт или ревизию электропроводки-80178.jpg)