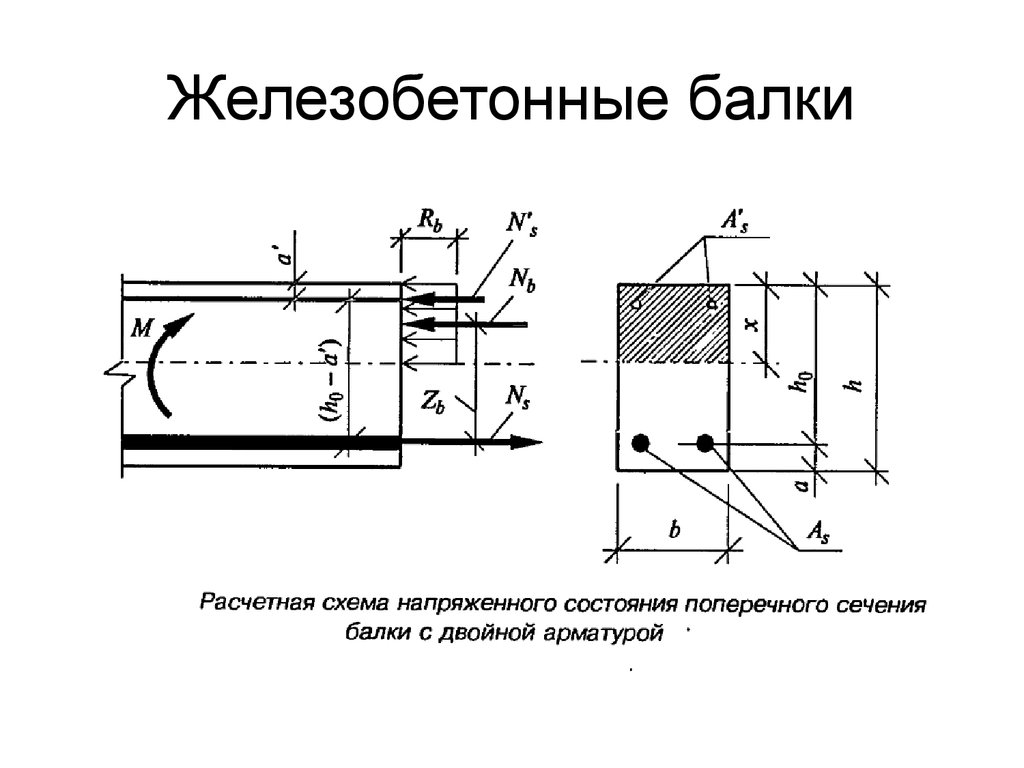
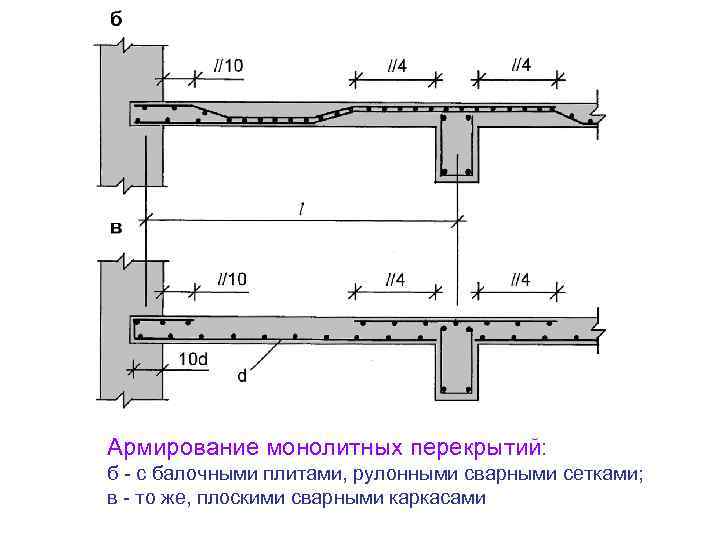
Расчет прочности балки прямоугольного сечения (СНиП)

Цель: Проверка режима экспертизы железобетона в постпроцессоре «Железобетон» вычислительного комплекса SCAD

Задача: Проверить прочность сечения консольной балки при заданном армировании

Ссылки: Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СНиП 2.03.01-84), 1989, с. 26.

Файл с исходными данными:

SCAD 3 SNiP.spr
отчет – SCAD 3 SNiP.doc

Соответствие нормативным документам: СНиП 2.03.01-84. 

Исходные данные:

Конструктивная группа Балка

Расстояние между арматурными стержнями в первом ряду S1  меньше допускаемого (см. п. 5.12 СНиП 2.03.01-84*).
Элементы: 1

Коэффициент надежности по ответственности  γ_n = 1
Коэффициент надежности по ответственности (2-е предельное состояние)  = 1
Тип элемента — Изгибаемый
Напряженное состояние — Одноосный изгиб

Бетон

Вид бетона: Тяжелый
Класс бетона: B25
Условия твердения: Естественное
Коэффициент условий твердения 1

Влажность воздуха окружающей среды — 40-75%

Трещиностойкость

Категория трещиностойкости — 3
Условия эксплуатации конструкции: В помещении
Режим влажности бетона — Естественная влажность
Допустимая ширина раскрытия трещин:
  Непродолжительное раскрытие  0,4 мм
  Продолжительное раскрытие  0,3 мм
 

Конструктивная группа Балка.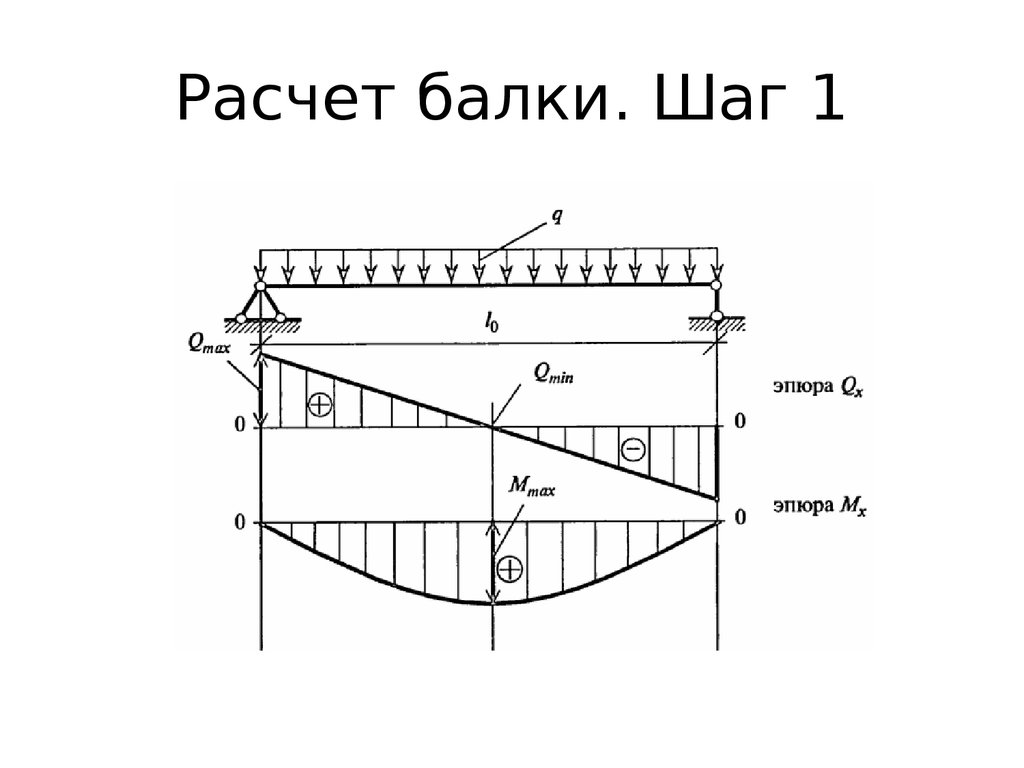 Элемент № 1
Длина элемента 5,0 м

Заданное армирование

Сравнение решений

Расчет ж/б балки прямоугольного сечения.

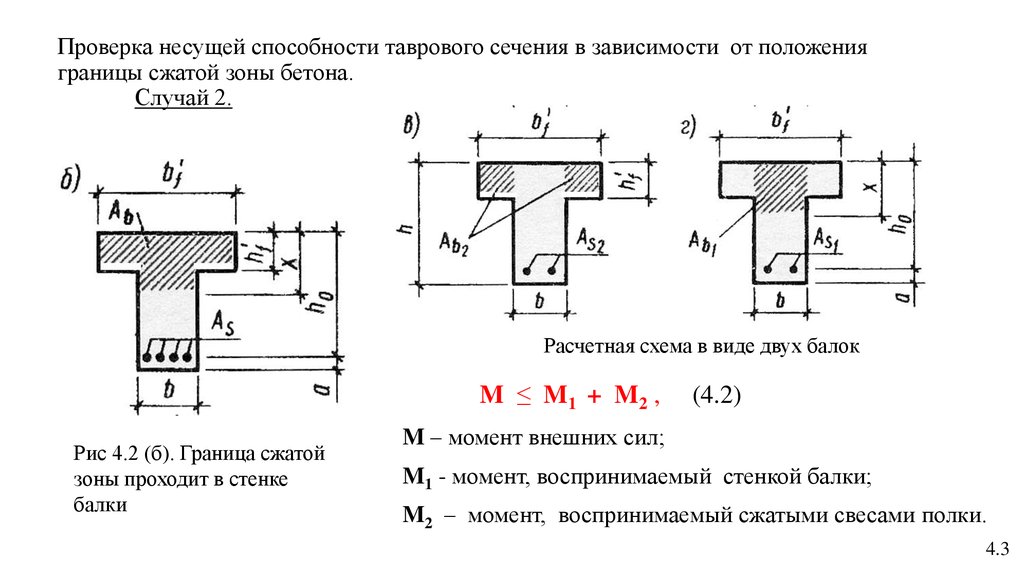Занятие 56. Практическая работа 8

Похожие презентации:

Творческий проект «Умный дом»

Грузоподъемные машины. (Лекция 4.1.2)

Основы архитектуры и строительных конструкций. Основы проектирования

Лакокрасочные материалы. Виды, состав

Металлические конструкции

Виды кранов

Общие сведения о кранах

Классификация крыш и покрытий

Фундамент. Классификация фундаментов

Свайные фундаменты. Классификация. (Лекция 6)

1. Практическая работа № 8

«Расчет ж/б балки прямоугольного сечения
• Основная идея расчёта сводится к тому, чтобы добиться баланса
между прочностью бетона на сжатие и прочностью арматуры на
растяжение.

3. Расчет:

•1. Геометрические параметры балки
•1.1. Определение длины балки.
• Рассчитать реальную длину балки проще всего. Главное, что мы
заранее знаем пролет, который должна перекрыть балка. Пролет это расстояние между несущими стенами для балки перекрытия
или ширина проема в стене для перемычки. Длина балки должна
быть больше пролета на ширину опирания на стены. Ширина опор
зависит от прочности материала конструкции под балкой и от
длины балки, чем прочнее материал конструкции под балкой и
чем меньше пролет, тем меньше может быть ширина опоры.
Теоретически рассчитать ширину опоры, зная материал
конструкции под опорой можно точно также, как и саму балку, но
обычно никто этого не делает, если есть возможность опереть
балку на кирпичные, каменные и бетонные (железобетонные)
стены на 150-300 мм при пролетах 2-10 метров. Для стен из
пустотелого кирпича и шлакоблока может потребоваться расчет
ширины опоры.

5. 1.2. Предварительное определение ширины и высоты балки и класс бетона, арматуры.

• «геометрические параметры зачастую нам заданы внешними факторами
и порой требуется посчитать, сможем ли мы вложиться в отведённое
нам пространство, а если не сможем, то сколько нужно арматуры»
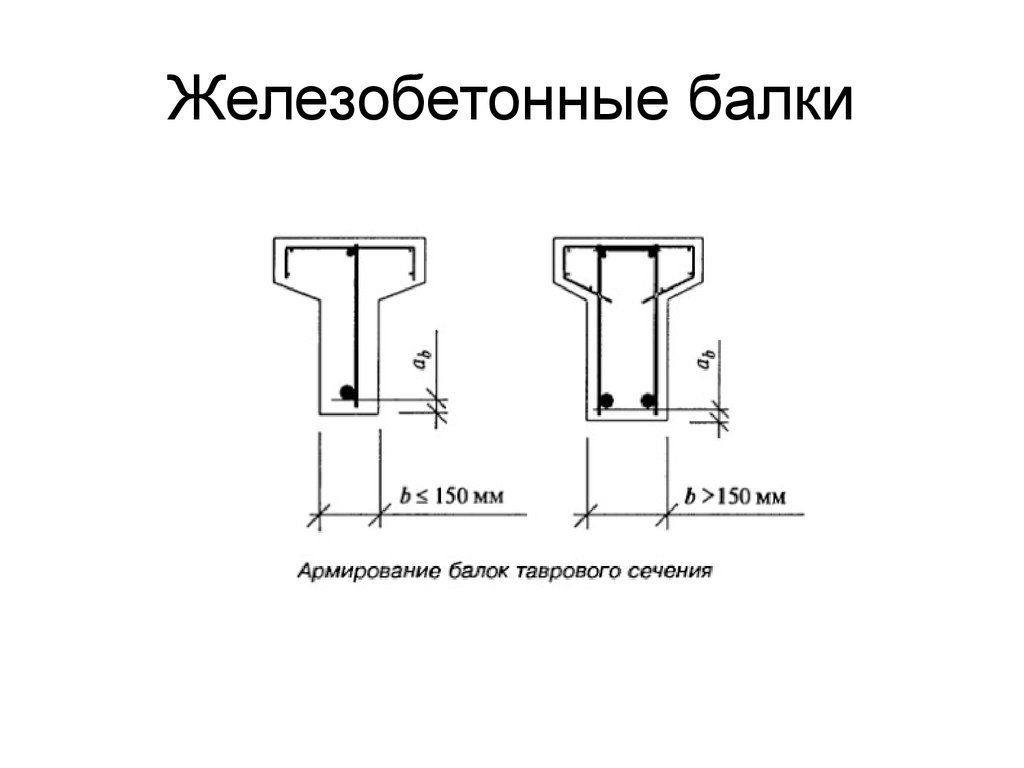
• Для балок перекрытия ширина может быть какой угодно, но обычно
принимается не менее 10 см и кратной 5 см (для простоты расчетов).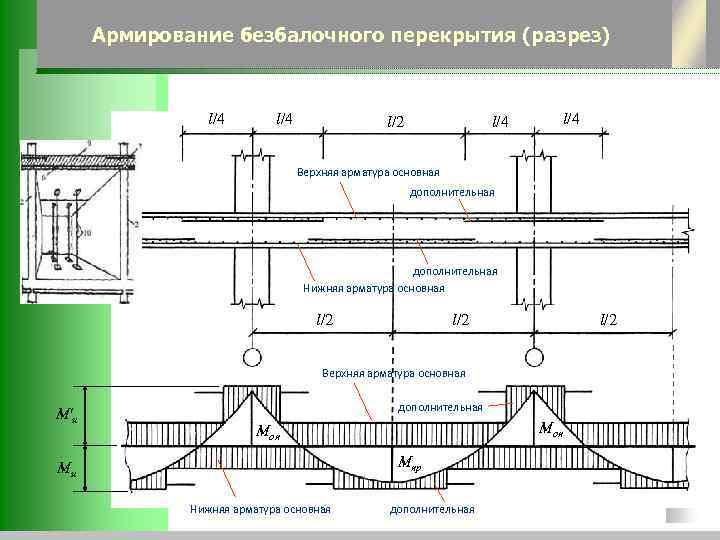
• Высота балки принимается из конструктивных или эстетических
соображений. Можно использовать пропорции: от 1/8L до 1/12L
• Класс бетона В20-В30

6. 2. Расчетная схема. Определение опор

• С точки зрения сопромата, будет ли это перемычка над
дверным или оконным проемом или балка перекрытия,
значения не имеет. А вот то как именно балка будет
опираться на стены имеет большое значение. С точки
зрения строительной физики любую реальную опору
можно рассматривать или как шарнирную опору, вокруг
которой балка может условно свободно вращаться или
как жесткую опору. Другими словами жесткая опора
называется защемлением на концах балки.

7. 1. Балка на двух шарнирных опорах.

Если железобетонная балка устанавливается в проектное
положение после изготовления, ширина опирания балки
на стены меньше 200 мм, при этом соотношение длины
балки к ширине опирания больше 15/1 и в конструкции
балки не предусмотрены закладные детали для жесткого
соединения с другими элементами конструкции, то такая
железобетонная балка однозначно должна
рассматриваться как балка на шарнирных опорах.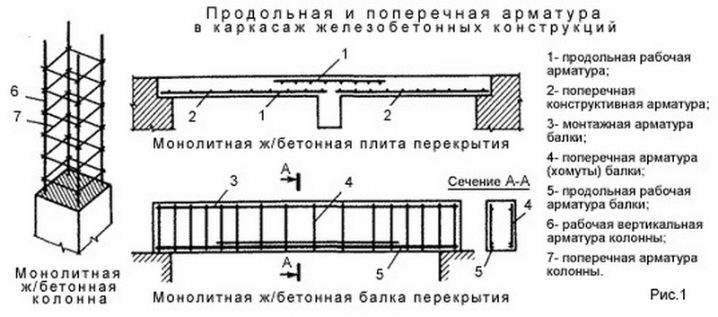 Для
такой балки принято следующее условное обозначение:

8. Балка на двух шарнирных опорах

9. 2. Балка с жестким защемлением на концах

• Если железобетонная балка изготавливается непосредственно в
месте установки, то такую балку можно рассматривать, как
защемленную на концах только в том случае, если и балка и
стены, на которые балка опирается, бетонируются
одновременно или при бетонировании балки предусмотрены
закладные детали для жесткого соединения с другими
элементами конструкции. Во всех остальных случаях балка
рассматривается, как лежащая на двух шарнирных опорах. Для
такой балки принято следующее условное обозначение:

10. 2. Балка с жестким защемлением на концах

11. 3. Многопролетная балка.

• Иногда возникает необходимость рассчитать железобетонную
балку перекрытия, которая будет перекрывать сразу две или даже
три комнаты, монолитное железобетонное перекрытие по
нескольким балкам перекрытия или перемычку над несколькими
смежными проемами в стене. В таких случаях балка
рассматривается как многопролетная, если опоры шарнирные. При
жестких опорах количество пролетов значения не имеет, так как
опоры жесткие, то каждая часть балки может рассматриваться и
рассчитываться как отдельная балка.

13. 4. Консольная балка

• Балка, один или два конца которой не имеют опор, а
опоры находятся на некотором расстоянии от концов
балки, называется консольной. Например плиту
перекрытия над фундаментом, выступающую за
пределы фундамента на несколько сантиметров,
можно рассматривать как консольную балку, кроме
того перемычку, опорные участки которой больше l/5
также можно рассматривать как консольную и так
далее.

14. Консольная балка.

15. 3. Определение нагрузки на балку 4. 5.

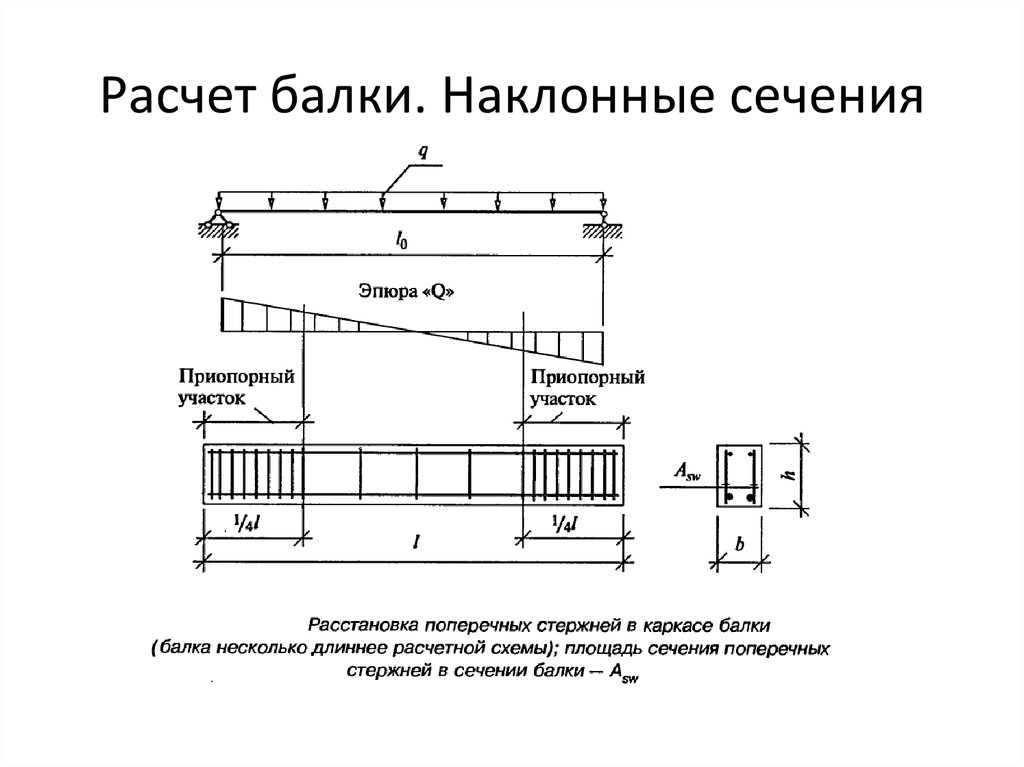
16. Проверка прочности по касательным напряжениям.

17. Прочность по наклонным сечениям

18. Ширина приопорных участков

19. Прогиб

•f = k5qlᶣ/384EIp
СП 20.13330.2016 Нагрузки и воздействия.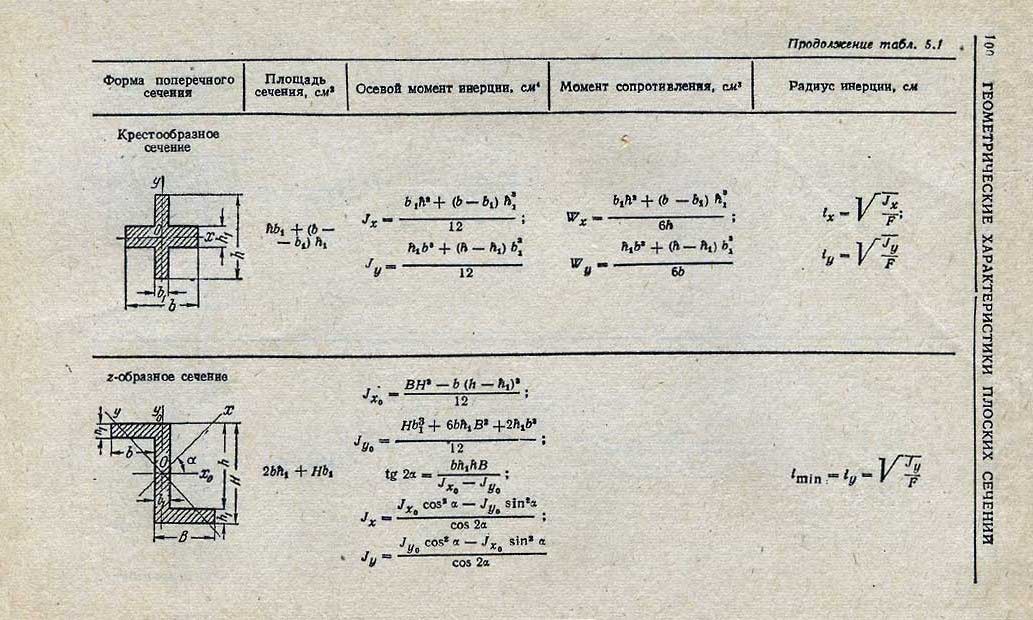
Актуализированная редакция СНиП 2.01.07-85*
(с Изменениями N 1, 2)
т. Д.1

English    
Русский
Правила

Калькулятор несущей способности бетонной балки

Калькулятор

Как пользоваться калькулятором

• Величины, отмеченные знаком «*», необходимы, без них расчеты не будут выполнены.
• Ширина (B), общая глубина (D) обязательны, длина не является обязательной и требуется только для определения безопасной нагрузки на балку.
• Марка бетона и марка стали также важны. Марка стали выбирается из выпадающего списка, и вы получаете 3 варианта марок: 250, 415 и 500.
• Для одноармированной балки сжатую арматуру нужно поставить 0, т.е. 0 номеров стержней.
• Выдержка должна быть выбрана по критерию долговечности и для указания номинального покрытия.
• Чистое покрытие и эффективное покрытие рассчитываются программой, однако пользователь может указать их и вручную.
• В результате эффективная глубина рассчитывается программой, однако пользователю предоставляется возможность указать пользовательскую эффективную глубину.

Что такое допустимый момент

Бетонная балка предназначена для сопротивления таким силам, как сдвиг, момент, кручение и т. д., которые удовлетворяют предельному состоянию разрушения. Момент несущей способности балки – это определение максимально допустимого безопасного момента, который может нести балка.

Это момент сопротивления, создаваемый блоком напряжения сжатия или блоком напряжения растяжения относительно нейтральной оси.

Вычислитель моментной прочности бетонной балки предназначен для нахождения момента сопротивления одноармированных и дважды армированных профилей в свободно опертом состоянии балки.

Одноармированная балка, воспринимающая момент

Одноармированная балка представляет собой бетонную балку с армированием только на растянутой стороне.

Шаг 1: Найдите фактическую нейтральную ось

Приравнивая блок напряжения сжатия к блоку напряжения растяжения, мы можем найти фактическую глубину нейтральной оси.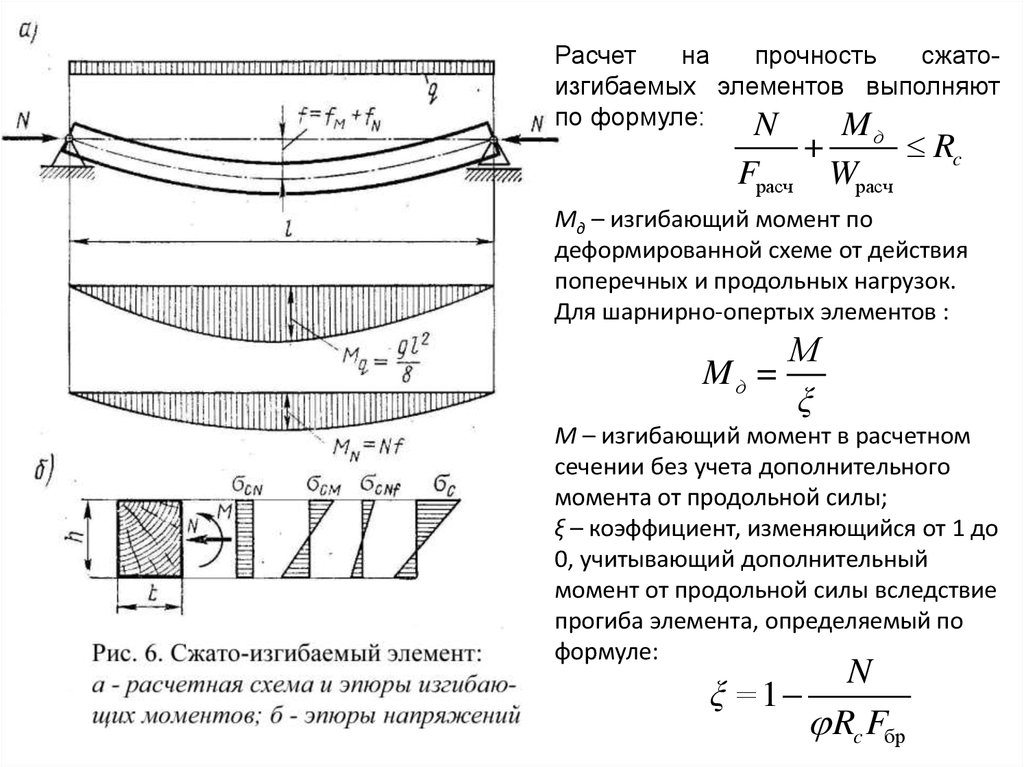

Шаг 2: Найдите максимальную глубину нейтральной оси

Максимальная глубина нейтральной оси зависит от марки используемой стали.

Формула допустимого момента зависит от того, больше ли фактическая нейтральная ось, чем максимальная нейтральная ось, или меньше, чем максимальная нейтральная ось.

Максимальная нейтральная ось также называется сбалансированной нейтральной осью.

Максимальная глубина нейтральной оси согласно IS 456:2000

1. Для Fe 250 = 0,53d
2. Для Fe 415 = 0,48d
3. Для Fe 500 = 0,46d

90 оси, то нейтральная ось должна быть ограничена максимальной нейтральной осью.

Шаг 3: Найдите момент сопротивления

Формула допустимого момента дается следующим образом:

Формула допустимого момента

Допустимый момент бетонной балки, когда нейтральная ось больше сбалансированной нейтральной оси, определяется следующим образом:

Допустимый момент формула для уравновешенного сечения

Балка с двойным армированием Допустимый момент

Балка с двойным армированием представляет собой бетонную балку, в которой армирование предусмотрено как на растяжение, так и на сжатие.

Шаг 1: Найдите фактическую нейтральную ось

Нейтральная ось сечения с двойным армированием для несущей способности бетонной балки задается следующим образом:

где fsc = напряжение в сжатой стали, fcc — напряжение в бетоне на уровне стали. Asc и Ast — это стали для сжатия и растяжения соответственно.

Шаг 2: Найдите максимальную глубину нейтральной оси

Этот шаг остается таким же, как и для одинарной армированной балки с максимальной нейтральной осью в зависимости от марки стали.

Шаг 3: Найдите момент сопротивления

Допустимый момент для бетонной балки с двойным армированием определяется следующим образом:

Расчет перемещений для рабочих нагрузок железобетонных балок и плит с использованием физически нелинейного анализа

. 2022 23 ноября; 15 (23): 8307.

дои: 10.3390/ma15238307.

Антонио Ренато Бичелли
¹
, Педро Кантор
¹
, Рафаэль Вонг
²
, Марио Руи Арруда
³


Принадлежности


• ¹ Instituto Superior Técnico, Universidade de Lisboa, 1049-001 Лиссабон, Португалия.
• ² Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa (UNL), 2825-149Капарика, Португалия.
• ³ CERIS-Instituto Superior Técnico, 1049-001 Лиссабон, Португалия.

• PMID:

  36499804

• PMCID:

  PMC9741035

• DOI:

  10.3390/ma15238307

Бесплатная статья ЧВК

Антонио Ренато Бичелли и др.

Материалы (Базель).

2022 .

Бесплатная статья ЧВК

. 2022 23 ноября; 15 (23): 8307.

дои: 10.3390/ma15238307.

Авторы


Антонио Ренато Бичелли
¹
, Педро Кантор
¹
, Рафаэль Вонг
²
, Марио Руи Арруда
³


Принадлежности


• ¹ Instituto Superior Técnico, Universidade de Lisboa, 1049-001 Лиссабон, Португалия.
• ² Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa (UNL), 2825-149Капарика, Португалия.
• ³ CERIS-Instituto Superior Técnico, 1049-001 Лиссабон, Португалия.

• PMID:

  36499804

• PMCID:

  PMC9741035

• DOI:

  10.3390/ma15238307

Абстрактный

Эта статья направлена ​​на использование нелинейного физического анализа для расчета смещения балок и плит в состоянии с трещинами. В этом исследовании используется коммерческое программное обеспечение SAP2000 для выполнения численного анализа с использованием формулы конечных элементов с применением многослойного метода. Первоначально было проведено параметрическое исследование для оценки вертикального смещения при эксплуатационных нагрузках железобетонных балок и плит с использованием различных пролетов, условий крепления и геометрии. Чтобы проверить модель конечных элементов, в исследовании сравнивались значения смещения для линейного анализа с использованием таблиц Бареса. В последующем применяются упрощенные методы расчета водоизмещения в перспективе с использованием счетов от Euro-International du Béton (CEB). Затем эти значения сравниваются с физически нелинейным анализом в состоянии длительного взлома с помощью SAP2000. В числовых и аналитических методах использовались два структурных кода, Regulamento de Estruturas de Betão Armado e Pré-Esforçado (REBAP) и Еврокод 2 (EC2), чтобы оценить их различия в контроле за деформацией. Таким образом, основная цель состоит в том, чтобы установить сравнения между двумя методами анализа, чтобы показать, что нелинейное моделирование методом конечных элементов обеспечивает значения, которые ниже, чем аналитический расчет, что позволяет добиться большей экономии при проектировании конструкционных железобетонных элементов. Кроме того, можно отметить, что EC2 имеет некоторые несоответствия в конструкции свободно опертых плит, требующих большей толщины, чем плоская квадратная плита, и что непрямая деформация для REBAP занижена для балок и, в некоторых случаях, для плит.


Ключевые слова:


треснувшее состояние; расчет водоизмещения; многослойный метод; физически нелинейный анализ.

Заявление о конфликте интересов


Авторы заявляют об отсутствии конфликта интересов.

Цифры


Рисунок 1

( a ) Минимальная толщина…

Рисунок 1

( a ) Минимальная толщина свободно опертой плиты и ( b…


фигура 1


( a ) Минимальная толщина свободно опертой плиты и ( b ) минимальная высота поддерживаемой балки.

Рисунок 2

( a ) Минимальная толщина…

Рисунок 2

( a ) Минимальная толщина опорной плиты с фиксированным концом и ( b…


фигура 2


( a ) Минимальная толщина плиты с фиксированным концом и ( b ) плиты с фиксированным концом.

Рисунок 3

Минимальная толщина квадрата…

Рисунок 3

Минимальная толщина квадратной плоской плиты.


Рисунок 3


Минимальная толщина квадратной плоской плиты.

Рисунок 4

Кривые напряжения-деформации для ( а…

Рисунок 4

Кривые напряжения-деформации для ( a ) бетона и ( b ) стали, оба…


Рисунок 4


Кривые напряжения-деформации для ( a ) бетона и ( b ) стали, обе адаптированы из [21].

Рисунок 5

( a ) Кривая импульс-кривизна…

Рисунок 5

( a ) Кривая импульс-кривизна железобетона, адаптированная из [21], ( b…


Рисунок 5


( a ) Кривая импульс-кривизна железобетона, адаптированная из [21], ( b ) Иллюстративный график ползучести, адаптированный из [22].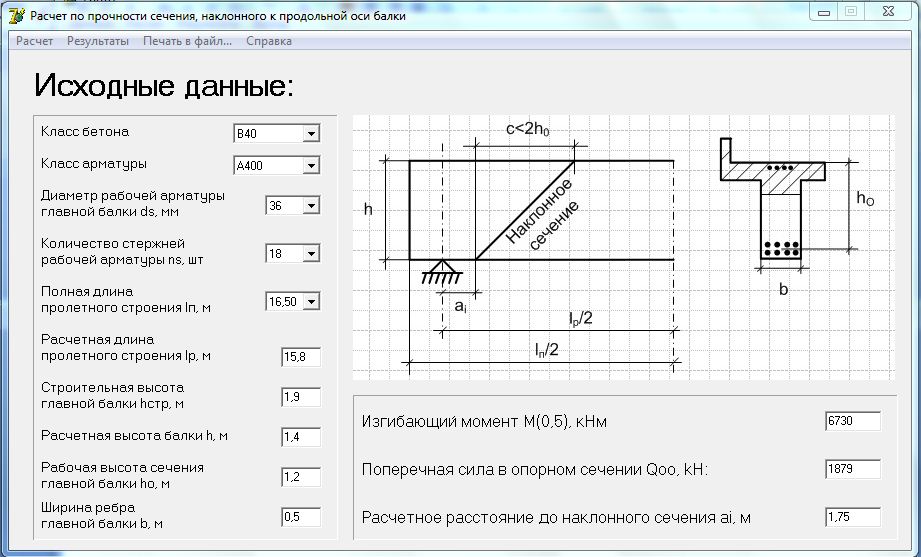 1 – безтрещинный режим, 2 – переходный режим, 3 – трещинный режим.

Рисунок 6

( a ) Просто поддерживается…

Рисунок 6

( a ) Свободно опертая балка с распределенной нагрузкой, ( b ) поперечное сечение…


Рисунок 6


( a ) Свободно опертая балка с распределенной нагрузкой, ( b ) поперечное напряжение в состоянии I и ( c ) в состоянии II.

Рисунок 7

( a ) Просто…

Рисунок 7

( a ) Плита с простой опорой и ( b ) с фиксированной опорой…


Рисунок 7


( a ) Просто поддерживаемая плита и ( b ) поддерживаемая неподвижная плита.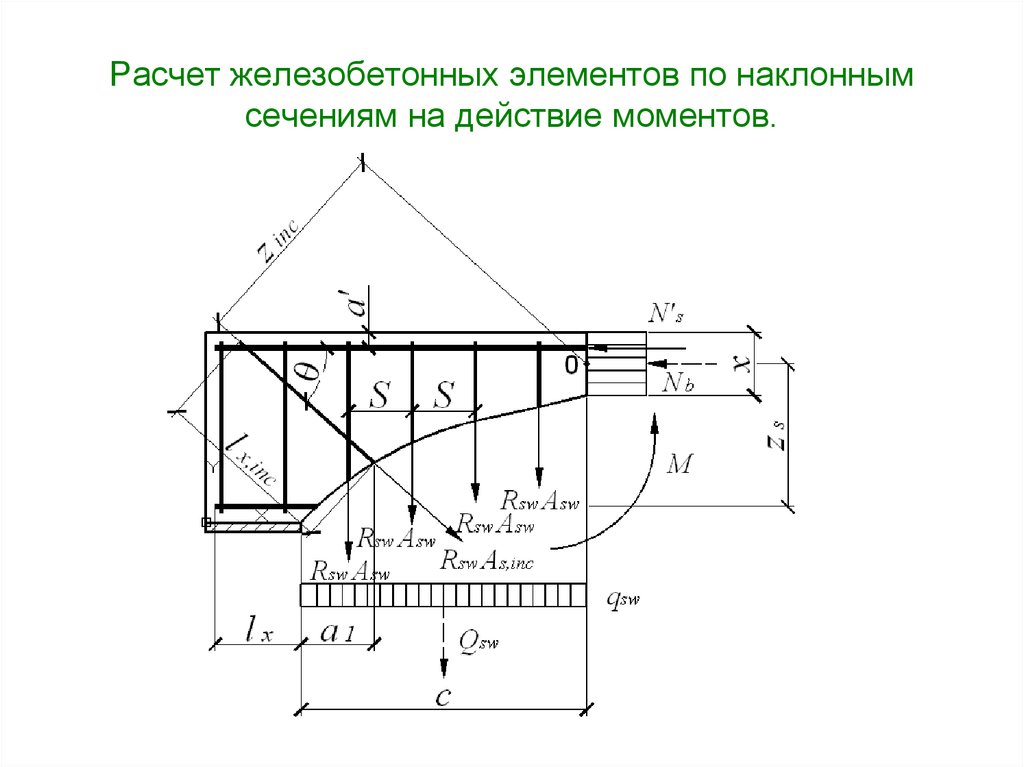

Рисунок 8

( a ) Плита с фиксированным концом…

Рисунок 8

( a ) Плита с фиксированным концом и ( b ) плоская плита.


Рисунок 8


( a ) Плита с фиксированным концом и ( b ) плоская плита.

Рисунок 9

Совместимость по рабочему объему в одной точке…

Рисунок 9

Совместимость смещения в одной точке для плиты с одним фиксированным краем.


Рисунок 9


Совместимость смещения в одной точке для плиты с одной фиксированной границей.

Рисунок 10

k коэффициент для ( a…

Рисунок 10

k коэффициент для ( a ) свободно опертой плиты, ( b ) поддерживаемой…


Рисунок 10


k коэффициент для ( a ) просто поддерживаемая плита, ( b ) поддерживаемая плита с фиксированными концами и ( c ) плита с фиксированными концами.

Рисунок 11

Сечение для ( и )…

Рисунок 11

Сечение для ( a ) железобетонной плиты и ( b ) нелинейных…


Рисунок 11


Поперечное сечение ( a ) железобетонной плиты и ( b ) нелинейного элемента оболочки.

Рисунок 12

Сечение для ( и )…

Рисунок 12

Сечение для ( a ) железобетонной балки и ( б ) нелинейный…


Рисунок 12


Поперечное сечение ( a ) железобетонной балки и ( b ) нелинейного элемента оболочки.

Рисунок 13

Распределение напряжения в трещине…

Рисунок 13

Распределение напряжений в поперечном сечении ж/б с трещинами с 10 слоями в SAP 2000.


Рисунок 13


Распределение напряжения в поперечном сечении ж/б с трещинами с 10 слоями в SAP 2000.

Рисунок 14

Кривые напряжения-деформации для ( a…

Рисунок 14

Кривые напряжения-деформации для ( a ) LM; ( б ) 1НЛМ; ( с…


Рисунок 14


Кривые напряжения-деформации для ( a ) LM; ( б ) 1НЛМ; ( c ) 2NLM и ( d ) стали, используемые в SAP2000 (значения в МПа и м/м).

Рисунок 15

Сетки конечных элементов для (…

Рисунок 15

Сетки конечных элементов для ( a ) балки и ( b ) плиты…


Рисунок 15


Сетки конечных элементов для моделей балок ( a ) и плит ( b ).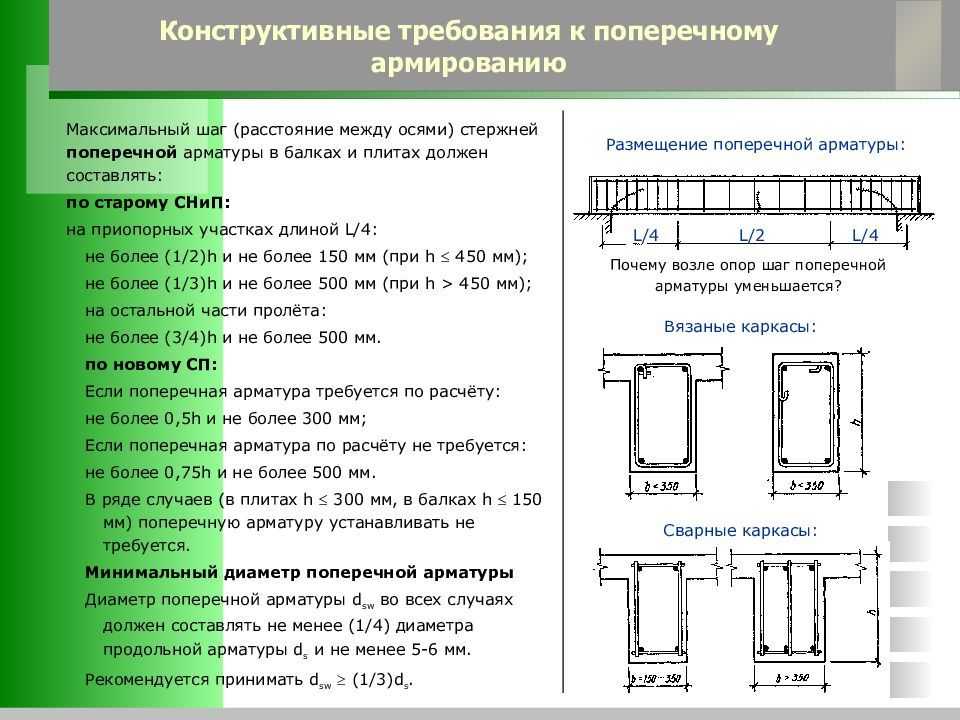

Рисунок 16

Схема соединения плиты с…

Рисунок 16

Схема соединения плиты с балкой в ​​конечно-элементной модели.


Рисунок 16


Схема соединения плиты с балкой в ​​конечно-элементной модели.

Рисунок 17

Схема для ( и )…

Рисунок 17

Схема для ( a ) просто опертая плита; ( b ) фиксированный с опорой…


Рисунок 17


Схема для ( a ) свободно опертой плиты; ( b ) плита с фиксированным концом; ( c ) плита с фиксированным концом и ( d ) плоская плита.

Рисунок 18

Значения соотношений для ( a…

Рисунок 18

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…


Рисунок 18


Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для свободно опертой плиты.

Рисунок 19

Значения деформации 2NLM: (…

Рисунок 19

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…


Рисунок 19


Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для свободно опертой плиты.

Рисунок 20

Значения соотношений для ( a…

Рисунок 20

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…


Рисунок 20


Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для плиты с фиксированным концом.

Рисунок 21

Значения деформации 2NLM: (…

Рисунок 21

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…


Рисунок 21


Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для плиты с фиксированными концами.

Рисунок 22

Значения соотношений для ( a…

Рисунок 22

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…


Рисунок 22


Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для плиты с фиксированными концами.

Рисунок 23

Значения деформации 2NLM: (…

Рисунок 23

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…


Рисунок 23


Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для плиты с фиксированными концами.

Рисунок 24

Значения соотношений для ( a…

Рисунок 24

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…


Рисунок 24


Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM, для плоской плиты.

Рисунок 25

Значения деформации 2NLM: (…

Рисунок 25

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…


Рисунок 25


Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для плоской плиты.

Рисунок 26

Значения соотношений для ( a…

Рисунок 26

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…


Рисунок 26


Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM, для опорной балки.

Рисунок 27

Значения деформации 2NLM: (…

Рисунок 27

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…


Рисунок 27


Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для поддерживаемой балки.

Рисунок 28

Сетка конечных элементов…

Рисунок 28

Сетка конечных элементов первого случая исследования.


Рисунок 28


Сетка конечных элементов первого случая исследования.

Рисунок 29

Сетка конечных элементов…

Рисунок 29

Сетка конечных элементов второго случая исследования.


Рисунок 29


Сетка конечных элементов второго случая исследования.

Рисунок 30

Сетка конечных элементов…

Рисунок 30

Сетка конечных элементов третьего случая исследования.


Рисунок 30


Сетка конечных элементов третьего случая исследования.

См. это изображение и информацию об авторских правах в PMC

Похожие статьи


• Конечно-элементное исследование структурного поведения армированного базальтовым волокном полимера (BFRP) — армированного самоуплотняющегося бетона (SCC) плит настила моста Томпсона.

  Чжоу Л., Чжэн Ю., Тейлор С.Э.
  Чжоу Л. и др.
  Полимеры (Базель). 2018 18 июня; 10 (6): 678. doi: 10.3390/polym10060678.
  Полимеры (Базель). 2018.

  PMID: 30966712
  Бесплатная статья ЧВК.

• Исследование ударопрочности железобетонных балок, усиленных полимерной сеткой, армированной углеродным волокном, и инженерными цементными композитами.

  Си З., Лю Ф., Пан Дж., Донг Х.
  Си З и др.
  Полимеры (Базель). 2022 11 мая; 14 (10): 1951. doi: 10.3390/polym14101951.
  Полимеры (Базель). 2022.

  PMID: 35631833
  Бесплатная статья ЧВК.

• Анализ прогиба многослойных плит с пластиковыми вставками.

  Масенас Ю., Шална Р., Юкнявичюс Л., Валивонис Ю.
  Масенас Дж. и др.
  Материалы (Базель). 2021 13 октября; 14 (20): 6050. дои: 10.3390/ma14206050.
  Материалы (Базель). 2021.

  PMID: 34683642
  Бесплатная статья ЧВК.

• Влияние геометрических ограничений на четырехточечное испытание удельного электрического сопротивления железобетонных плит Веннера.

  Роблес КПВ, Йи Дж.Дж., Ки Ш.Х.
  Роблес КПВ и др.
  Датчики (Базель). 2021 5 июля; 21 (13): 4622. дои: 10.3390/s21134622.
  Датчики (Базель). 2021.

  PMID: 34283169
  Бесплатная статья ЧВК.

• Экспериментальные данные и подтверждение поведения при кручении фибробетонных балок: обзор.

  Awoyera PO, Effiong JU, Olalusi OB, Prakash Arunachalam K, de Azevedo ARG, Martinelli FRB, Monteiro SN.
  Awoyera PO и соавт.
  Полимеры (Базель). 2022 15 марта; 14 (6): 1171. дои: 10.3390/polym14061171.
  Полимеры (Базель). 2022.

  PMID: 35335504
  Бесплатная статья ЧВК.

  Обзор.

Посмотреть все похожие статьи

использованная литература


1. 1. Bathe K.-J., Walczak J., Welch A., Mistry N. Нелинейный анализ бетонных конструкций. вычисл. Структура 1989; 32: 563–590. doi: 10.1016/0045-7949(89)

      -7.

      —

      DOI

2. 1. Хсу Ц.