Таблица перевода куба
- Главная
- Библиотека
- Строительные калькуляторы
- Калькуляторы мер длин
- Объявления
- FAQ
- Статьи
Все о стройке » Таблица перевода куба
Значительная часть строительных работ требует измерение в единицах объема. Это, прежде всего, бетонирование и кирпичная кладка, земля-ные работы. Зачастую, количество привезенных материалов измеряется в кубических единицах, также в них может измеряться объем вывезенного мусора. И при проектировании, и на строительстве, и в процессе лабораторных исследований пригодится настоящая таблица перевода единиц объема.
В таблице представлены соотношения следующих кубических единиц: кубический метр, кубический дециметр, кубический сантиметр, кубический миллиметр, гекто-литр, декалитр, литр, децилитр, сантилитр, миллилитр и микролитр.
Некоторые из приведенных единиц на практике встречаются редко, но таблица без них не была бы полной.
Для каждой единицы объема составлена отдельная таблица перевода в другие единицы через коэффициенты.
Пример: Требуется выразить величину 0,6 м3 в других единицах измерения.
Рассмотрим таблицу соответствия 1 квадратного метра и поочеред-но перемножим наше значение на коэффициенты перевода.
- В результате расчетов определяем, что 0,6 м2 составляет:
- 600 кубических дециметров;
- 600000 или 6×105 кубических сантиметров;
- 6×108 кубических миллиметров;
- 6 гектолитров;
- 60 декалитров;
- 600 литров;
- 6000 децилитров;
- 60000 сантилитров;
- 600000 миллилитров;
- 6×108 микролитров.
1 кубический метр | |
|---|---|
| Метрическая мера | |
| кубический дециметр | 1000 |
| кубический сантиметр | 1000000 |
| кубический миллиметр | 1×109 |
| гектолитр | 10 |
| декалитр | 100 |
| литр | 1000 |
| децилитр | 10000 |
| сантилитр | 100000 |
| миллилитр | 1000000 |
| микролитр | 1×109 |
1 кубический дециметр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 0.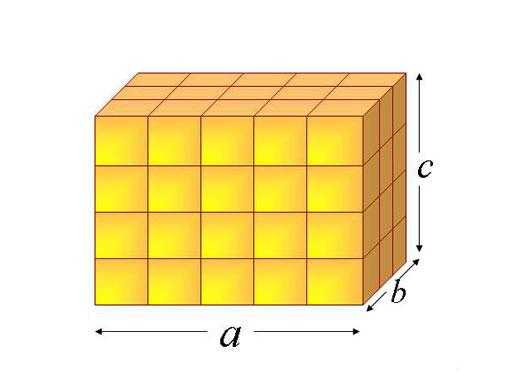 001 001 |
| кубический сантиметр | 1000 |
| кубический миллиметр | 1000000 |
| гектолитр | 0.01 |
| декалитр | 0.1 |
| литр | 1 |
| децилитр | 10 |
| сантилитр | 100 |
| миллилитр | 1000 |
| микролитр | 1000000 |
1 кубический сантиметр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 1×10-6 |
| кубический дециметр | 0.001 |
| кубический миллиметр | 1000 |
| гектолитр | 1×10-5 |
| декалитр | 0.0001 |
| литр | 0.001 |
| децилитр | 0.01 |
| сантилитр | 0.1 |
| миллилитр | 1 |
| микролитр | 100 |
1 кубический миллиметр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 1×10-9 |
| кубический дециметр | 1×10-6 |
| кубический сантиметр | 0. 001 001 |
| гектолитр | 1×10-8 |
| декалитр | 1×10-7 |
| литр | 1×10-6 |
| децилитр | 1×10-5 |
| сантилитр | 0.0001 |
| миллилитр | 0.001 |
| микролитр | 1 |
1 гектолитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 0.1 |
| кубический дециметр | 100 |
| кубический сантиметр | 100000 |
| кубический миллиметр | 1×108 |
| декалитр | 10 |
| литр | 100 |
| децилитр | 1000 |
| сантилитр | 10000 |
| миллилитр | 100000 |
| микролитр | 1×108 |
1 декалитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 0. 01 01 |
| кубический дециметр | 10 |
| кубический сантиметр | 10000 |
| кубический миллиметр | 1×107 |
| гектолитр | 0.1 |
| литр | 10 |
| децилитр | 100 |
| сантилитр | 1000 |
| миллилитр | 10000 |
| микролитр | 1×107 |
1 литр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 0.001 |
| кубический дециметр | 1 |
| кубический сантиметр | 1000 |
| кубический миллиметр | 1000000 |
| гектолитр | 0.01 |
| декалитр | 0.1 |
| децилитр | 10 |
| сантилитр | 100 |
| миллилитр | 1000 |
| микролитр | 1000000 |
1 децилитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 0.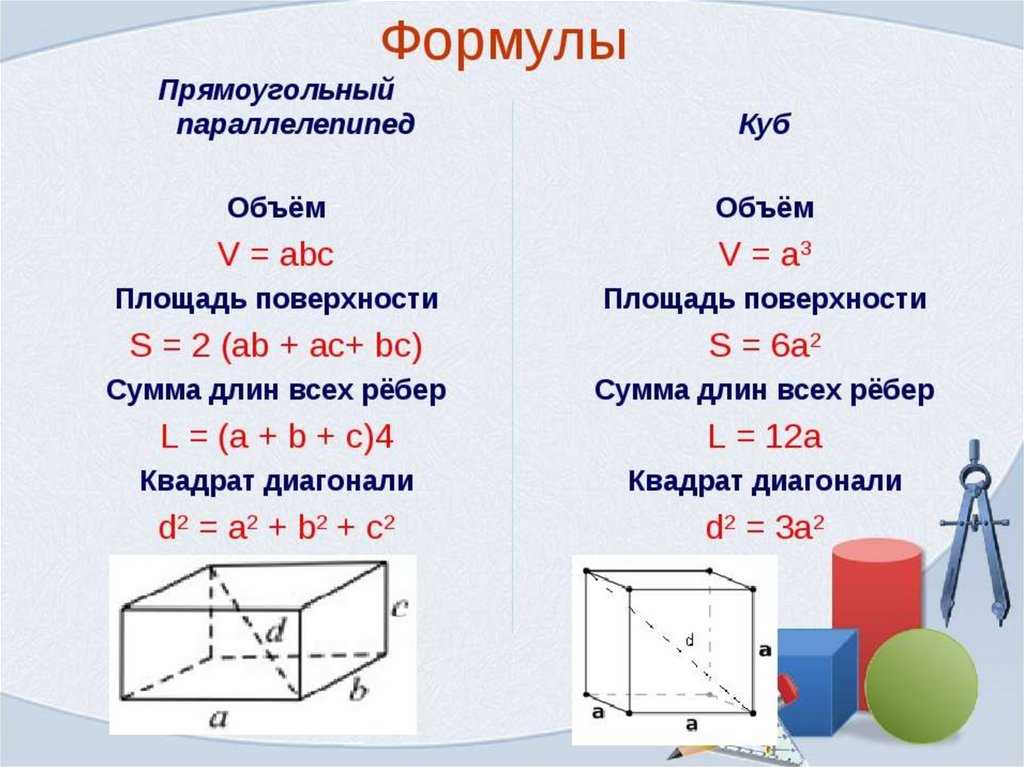 0001 0001 |
| кубический дециметр | 0.1 |
| кубический сантиметр | 100 |
| кубический миллиметр | 100000 |
| гектолитр | 0.001 |
| декалитр | 0.01 |
| литр | 0.1 |
| сантилитр | 10 |
| миллилитр | 100 |
| микролитр | 100000 |
1 сантилитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 1×10-5 |
| кубический дециметр | 0.01 |
| кубический сантиметр | 10 |
| кубический миллиметр | 10000 |
| гектолитр | 0.0001 |
| декалитр | 0.001 |
| литр | 0.01 |
| децилитр | 0.1 |
| миллилитр | 10 |
| микролитр | 10000 |
1 миллилитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 1×10-6 |
| кубический дециметр | 0. 001 001 |
| кубический сантиметр | 1 |
| кубический миллиметр | 1000 |
| гектолитр | 1×10-5 |
| декалитр | 0.0001 |
| литр | 0.001 |
| децилитр | 0.01 |
| сантилитр | 0.1 |
| микролитр | 1000 |
1 микролитр соответствует: | |
|---|---|
| Метрическая мера | |
| кубический метр | 1×10-9 |
| кубический дециметр | 1×10-6 |
| кубический сантиметр | 0.001 |
| кубический миллиметр | 1 |
| гектолитр | 1×10-8 |
| декалитр | 1×10-7 |
| литр | 1×10-6 |
| децилитр | 1×10-5 |
| сантилитр | 0. 0001 0001 |
| миллилитр | 0.001 |
Как определить куб дров (кубатуру) или объем при покупке
Закупка дров всегда связана с определением объема. У продавцов существуют несколько способов продажи.
На складе дрова могут быть уложены в штабеля, но конечному покупателю они продаются навалом прямо с кузова грузовика. Это затрудняет точное определение объема привезенных дров.
Возрастает вероятность заплатить денег за больший объем дров, чем привезли на самом деле. Недобросовестные продавцы часто этим пользуются.
Для определения приблизительного объема закупаемых дров необходимо знать методы замеров.
В конце размещен калькулятор расчета кубатуры дров.
Содержание
- 1 Как измеряется объем дров
- 1.1 Способы расчета кубатуры дров
- Реальный кубический метр — для древесины уложенной в штабеля без промежутков.
- Складочный кубический метр — для кругляка, учитывает промежутки.

Способы расчета кубатуры дров
- Объем сплошной древесины пиломатериала, который аккуратно складирован в штабель, определить несложно обычным измерением длины, ширины и высоты штабеля. Перемножение полученных значений и является объемом дров в кубометрах.
- Для круглого леса объем рассчитывается как произведение длины бревна и его среднего диаметра.
- Для определения объема колотых дров или дров в чурках применяется складочный кубометр. Этот объем определяется методом измерения длины, ширины и высоты укладки поленьев, но при пересчете применяется поправочный коэффициент. Обычно он равен 0,7.
Если взять 5 складочных кубометров дров и 5 кубометров уложенного пиломатериала, то они должны приблизительно быть одинаковыми по количеству древесины.
Очень часто дрова продают без укладки, и определить объем насыпной древесины намного сложнее. Для этого применяют понятие насыпного или навального кубометра. Такая мера измерения применяется при транспортировке дров навалом в кузове автомобиля или другого транспортного средства.
Такая мера измерения применяется при транспортировке дров навалом в кузове автомобиля или другого транспортного средства.
Объем дров при этом определяется следующим образом:
- Необходимо посчитать объем кузова (перемножив его длину, ширину и высоту) и тем самым, определим объем в складочных кубометрах.
- Перемножить на поправочный коэффициент.
Это и будет объемом дров в навальных кубометрах.
Зависимость коэффициента от длины поленьев сведена в таблицу:
| Длина полена в метрах | Коэффициент пересчета |
| 0,25 | 0,8 |
| 0,33 | 0,78 |
| 0,50 | 0,75 |
| 0,75 | 0,73 |
Также дрова продаются такими мерами объема, как телега, газон, камаз. Ни один продавец при этом вам не скажет истинного объема дров в кузове.
Ни один продавец при этом вам не скажет истинного объема дров в кузове.
Намного удобнее и проще было бы покупать дрова по массе, но тут также встает вопрос с влажностью, которую еще сложнее оценить.
Читайте также, как влияет плотность и влажность, порода древесины на теплотворную способность дров.
Но альтернатива есть. К примеру, древесные брикеты продаются килограммами, тоннами. Тут уж ошибиться можно только с весами.
Что такое топливные брикеты или еще их называют евродрова.
Какие бывают виды брикетов.
Что лучше для отопления дома брикеты или дрова.
Что такое кубические единицы? Определение, формула, объем, примеры
Что такое кубическая единица?
Кубическая единица — это единица измерения объема.
Другими словами, эти единицы являются способом измерения пространства, занимаемого чем-либо.
Подумайте о книге: Каков ее объем? Его объем зависит от длины, ширины и высоты. Умножение этих трех линейных измерений дает нам кубическое измерение.
Умножение этих трех линейных измерений дает нам кубическое измерение.
Объем относится к пространству, занимаемому объектом или трехмерной фигурой. Измеряется в кубических единицах.
Точно так же объем воды в бассейне можно измерить в кубических единицах.
Определение кубических единиц
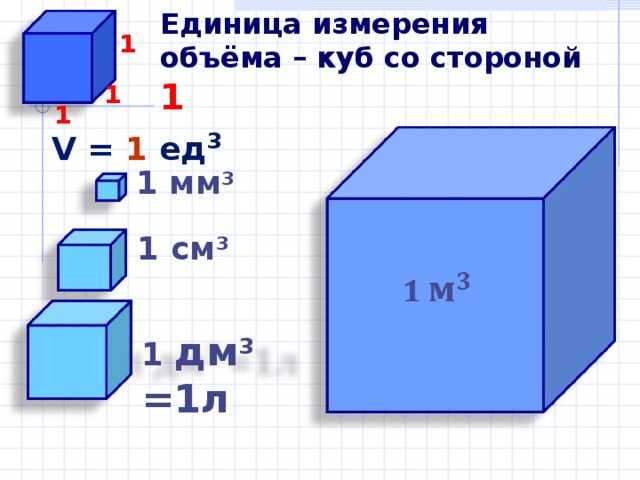
В геометрии кубические единицы могут быть определены как единицы, используемые для измерения объема. Объем единичного куба, длина, ширина и высота которого равны 1 единице, равен 1 кубической единице.
Обозначение кубических единиц может быть указано как единица 3 . Например, «кубический сантиметр» можно представить как см 3 .
Обычные единицы измерения, такие как дюймы, футы, ярды, мили, сантиметры, метры и километры, описывают стороны фигуры, как стороны прямоугольника. Кубические единицы измеряют трехмерное пространство или объем.
Как работает кубическая единица?
Каждое измерение куба единиц (длина, ширина и высота) является одной единицей.
Итак, одна единица длины с одной единицей ширины и одной единицей высоты вместе составляют объем одной кубической единицы .
Когда мы измеряем объем, мы измеряем его с точки зрения того, сколько «единичных кубов» по 1 кубической единице объема каждый поместится в этом объеме, если мы поместим их рядом или один над другим.
На изображении ниже мы можем найти объем данной фигуры, подсчитав общее количество кубических единиц. Он состоит из $10 \times 10$ кубических единиц. Значит объем фигуры 100 кубических единиц.
При расчете объема чего-либо в кубических единицах вы должны умножить значение каждого измерения (длины, ширины и высоты).
Длина, ширина и высота измеряются в отдельных единицах, таких как дюймы, футы и ярды или сантиметры и метры.
Например, на приведенном ниже рисунке прямоугольный параллелепипед состоит из меньших единичных кубов. Кубоид имеет длину 6 дюймов, высоту 4 дюйма и ширину 2 дюйма.
При перемножении размеров получается объем, выраженный в кубических единицах (таких как кубические дюймы, кубические футы, кубические ярды, кубические сантиметры или кубические метры).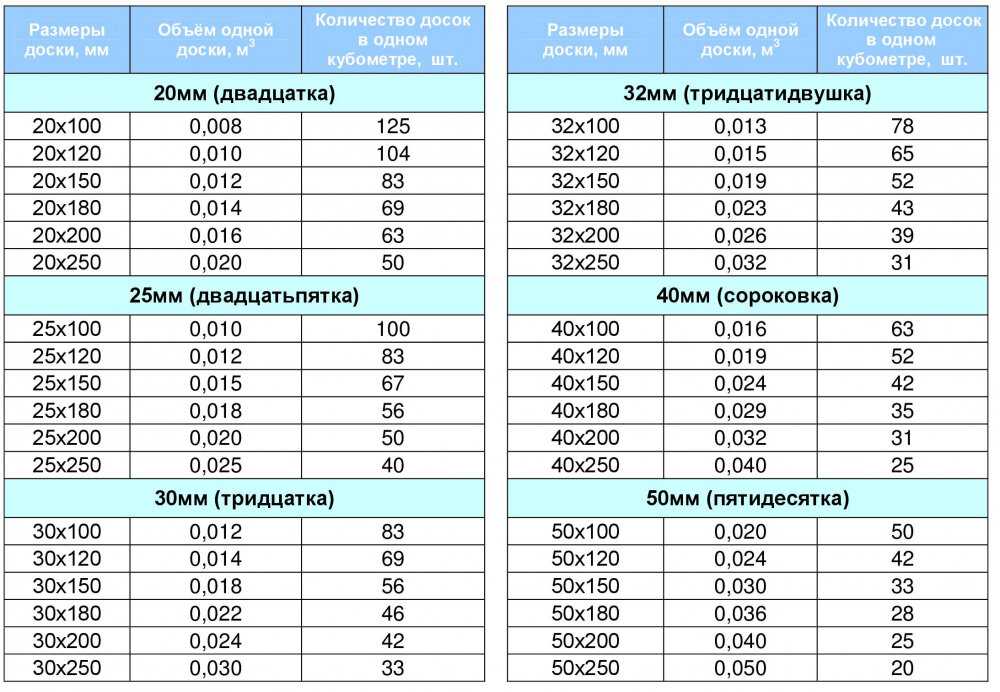
Умножение размеров прямоугольного параллелепипеда:
$6$ $\text{дюймы} \times 4$ $\text{дюймы} \times 2$ $\text{дюймы} = 48$ $\text{кубические дюймы}$
48 кубических дюймов — это объем в кубических единицах.
Длину, ширину и высоту прямоугольного параллелепипеда также можно измерить, подсчитав количество единичных кубов. Затем объем определяется в кубических единицах.
Попробуем другой пример. Если сторона куба 5 дм, то каков будет его объем?
Объем куба $= \text{length} \times \text{width} \times \text{height}$
Поскольку длина, ширина и высота в кубе равны, объем будет:
$5 \times 5 \times 5 = 125$ кубических дюймов.
Мы видим, что единица измерения дюймов меняется на кубические дюймы.
Некоторыми примерами кубических единиц в метрических единицах являются кубические метры и кубические сантиметры, а в обычных единицах измерения — кубические дюймы и кубические футы.
Такие единицы, как квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, квадратные сантиметры, квадратные метры и квадратные километры, описывают площадь фигуры и используются для измерения двумерных фигур или площадей.
Кубические единицы, такие как кубические дюймы, кубические футы, кубические сантиметры и кубические метры, измеряют трехмерное пространство или объем.
Кубические преобразования
Мы можем преобразовать одну кубическую единицу (например, кубические дюймы) в другую кубическую единицу (например, кубические футы).
Некоторые приблизительные преобразования для кубических единиц приведены ниже:
1 кубический дюйм $ = 0,0006 $ кубических футов
1 кубический дюйм $ = 0,00002 $ кубических ярдов
1 кубический дюйм $ = 16,39 $ кубических сантиметров
1 кубический дюйм $= 0,000016$ кубических метров
1 кубический фут $= 1728$ кубических дюймов
1 кубический фут $= 0,037$ кубических ярдов
1 кубический фут $= 28316,85$ кубических футов 1 $
7 = 0,028$ кубических метров
1 кубический сантиметр $= 0,000001$ кубических метров
1 кубический сантиметр $= 0,061$ кубических дюймов
1 кубический сантиметр $= 0,000035$ куб.
1 кубический метр $ = 1 000 000 $ кубических сантиметров
1 кубический метр $= 61023,7$ кубических дюймов
1 кубический метр $= 35,3$ кубических футов
1 кубический метр $= 1,31$ кубических ярдов
Решаемые примеры
1. Сколько стоит каждая сторона единицы кубическая мера?
Раствор : 1 шт. Единичный куб имеет длину, ширину и высоту, равные одной единице.
2. Книга имеет длину 12 дюймов, ширину 10 дюймов и высоту 4 дюйма. Каков его объем?
Решение : Объем книги $= \text{длина} \times \text{ширина} \times \text{высота}$
$= 12$ $\text{дюймов} \times 10$ $\text {inches} \times 4$ $\text{inches}$
$= 480$ кубических дюймов
Объем книги 480 кубических дюймов.
3. Сколько кубических дюймов составляет один кубический фут?
Решение : 1 фут $= 12$ дюймов
1 кубический фут $= 1$ $\text{фут} \times 1$ $\text{фут} \times 1$ $\text{фут}$
Таким образом, 1 кубический фут $= 12$ $\text{дюймы} \times 12$ $\text{дюймы} \times 12$ $\text{дюймы}$
$= 1728$ кубические дюймы
Практические задачи
1
Сколько кубических футов составляет один кубический ярд?
3 кубических фута
10 кубических футов
27 кубических футов
9 кубических футов
Правильный ответ: 27 кубических футов
1 ярд $= 3$ футов
1 кубический ярд $= 3$ $\text{футы } \times 3$ $\text{футы} \times 3$ $\text{футы}$
$= 27$ кубических футов
2
Каков объем пол-литра молока?
5000 мл
500 кубических метров
0,005 кубические метры
0,0005 кубические метры
Правильный ответ: 0,0005 кубических метров
1 кубический метр $ = 1000 $ Liters
SO 1 литр $ 0,001 $ Cubic Metters
$ Litters
SO 1 литр $ 0,001 $ Кубические метры
$. 0,5 литра $= 0,0005$ кубических метров
0,5 литра $= 0,0005$ кубических метров
3
Классная комната имеет длину 10 ярдов, ширину 8 ярдов и высоту 6 ярдов. Каков объем класса?
60 куб. ярдов
80 куб. ярдов
480 куб. ярдов
480 ярдов
Правильный ответ: 480 куб. text{yards} \times 6$ $\text{yards}$
$= 480$ кубических ярдов
4
Сторона кубического ящика равна 0,5 фута. Вычислите объем в кубических футах.
0,25 куб. фута
0,125 куб. фута
1,25 куб. фута
12,5 куб. фута
Правильный ответ: 0,125 кубических фута
Поскольку это кубическая коробка, длина, ширина и высота равны, поэтому все они равны 0,5 фута.
Объем кубического ящика $= 0,5$ $\text{футы} \times 0,5$ $\text{футы} \times 0,5$ $\text{футы}$
$= 0,125$ кубические футы
Часто задаваемые вопросы
Почему важны кубические единицы?
Кубические единицы важны, потому что они представляют стандартные единицы объема.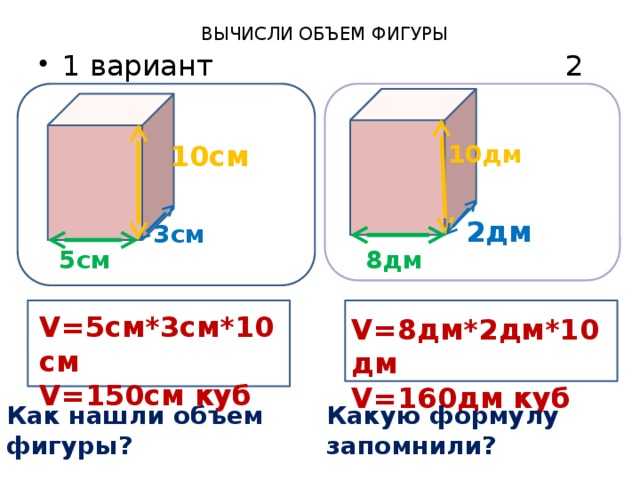 Это помогает нам измерять объем в разных единицах, таких как кубические дюймы или кубические сантиметры.
Это помогает нам измерять объем в разных единицах, таких как кубические дюймы или кубические сантиметры.
Можем ли мы использовать кубические единицы для измерения объема трехмерных фигур, отличных от куба?
Да, кубические единицы можно использовать для измерения объема различных трехмерных фигур, таких как сфера, прямоугольный параллелепипед или призма.
Кубические единицы используются для измерения общего занимаемого пространства, поэтому форма фигуры не имеет значения.
Можно ли использовать кубические единицы для измерения объема жидкостей?
Да, мы можем использовать кубические единицы для измерения объема жидкостей.
Мы делаем это путем преобразования единиц объема жидкости, таких как литры или мл, в кубические единицы, такие как кубические метры.
Объем куба — формула, определение, решенные примеры
Объем куба определяется как общее количество кубических единиц, полностью занимаемых кубом.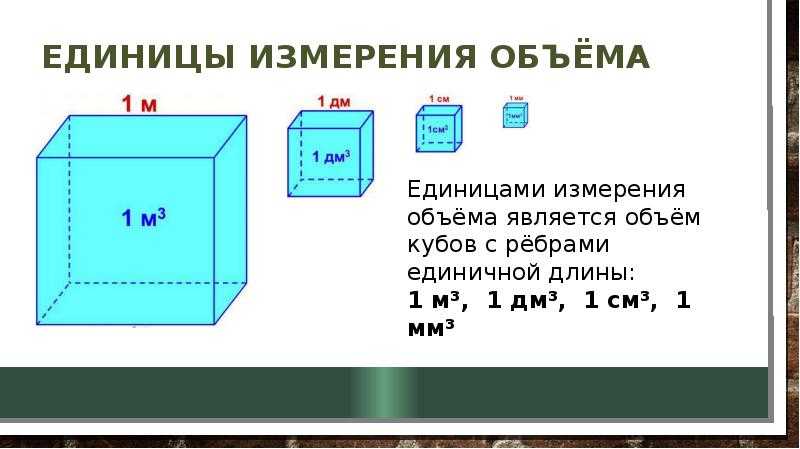 Куб — объемная объемная фигура, имеющая 6 квадратных граней. Объем — это не что иное, как общее пространство, занимаемое объектом. Объект большего объема занял бы больше места. Давайте подробно разберемся с объемом куба вместе с формулой и решенными примерами в следующих разделах.
Куб — объемная объемная фигура, имеющая 6 квадратных граней. Объем — это не что иное, как общее пространство, занимаемое объектом. Объект большего объема занял бы больше места. Давайте подробно разберемся с объемом куба вместе с формулой и решенными примерами в следующих разделах.
| 1. | Что такое объем куба? |
| 2. | Формула объема куба |
| 3. | Как найти объем куба? |
| 4. | Часто задаваемые вопросы о Volume of Cube |
Что такое объем куба?
Объем куба — это общее трехмерное пространство, занимаемое кубом. Куб — это трехмерный твердый объект с шестью квадратными гранями, имеющими все стороны одинаковой длины. Куб также известен как правильный шестигранник и является одной из пяти платоновых тел. Единицей объема куба является (единица) 3 или кубических единиц. Единицей объема в СИ является кубический метр (м 3 ), который представляет собой объем, занимаемый кубом, каждая сторона которого равна 1 м. Единицы объема USCS: дюймы 3 , ярды 3 и т. д.
Единицей объема в СИ является кубический метр (м 3 ), который представляет собой объем, занимаемый кубом, каждая сторона которого равна 1 м. Единицы объема USCS: дюймы 3 , ярды 3 и т. д.
Объем формулы куба
Объем любого куба можно рассчитать по разным формулам на основе заданных параметров. Его можно рассчитать, используя длину стороны или размер диагонали куба.
Объем куба с использованием формулы стороны
Объем куба можно найти, трижды умножив длину ребра. Например, если длина ребра куба равна 4, объем будет равен 4 3 . Формула для расчета объема куба дается как,
Объем куба = s 3 , где s — длина стороны куба.
Принцип получения формулы объема куба можно понять, выполнив следующие шаги:
- Рассмотрим любой лист бумаги квадратной формы.
- Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е.
 его длине, умноженной на его ширину. Что касается квадрата, так как длина и ширина равны, площадь поверхности будет «s 2 ».
его длине, умноженной на его ширину. Что касается квадрата, так как длина и ширина равны, площадь поверхности будет «s 2 ». - Куб получается путем складывания нескольких квадратных листов друг на друга так, чтобы высота стала равной длине и ширине, т. е. единицам «s».
- Это дает нам высоту или толщину куба как «s».
- Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, будет равно площади основания, умноженной на высоту.
Объем куба по формуле для диагонали
Объем куба также можно определить непосредственно по другой формуле, если известна диагональ.
Диагональ куба определяется как √3s, где s — длина стороны куба. Из этой формулы мы можем записать «s» как s = диагональ/√3.
Таким образом, объем уравнения куба с использованием диагонали можно окончательно определить как:
Объем куба = (√3×d 3 )/9
где d — длина диагонали куба.
Примечание: Следует избегать распространенной ошибки, не путая диагональ куба с диагональю его грани. Диагональ куба проходит через его центр, как показано на рисунке выше. В то время как диагональ грани — это диагональ на каждой грани куба.
Диагональ куба проходит через его центр, как показано на рисунке выше. В то время как диагональ грани — это диагональ на каждой грани куба.
Как найти объем куба?
Объем куба можно легко узнать, зная только длину его ребра или длину его диагонали. В этом разделе будут рассмотрены различные шаги, которые необходимо выполнить для вычисления площади куба в зависимости от заданных параметров.
Объем куба с использованием длины ребра
Меры всех сторон куба одинаковы, поэтому нам нужно знать только одну сторону, чтобы вычислить объем куба. Шаги для расчета объема куба с использованием длины стороны:
- Шаг 1: Обратите внимание на измерение длины стороны куба.
- Шаг 2: Примените формулу для расчета объема с использованием длины стороны: Объем куба = (сторона) 3 .
- Шаг 3: Выразите окончательный ответ вместе с единицей (кубическими единицами), чтобы представить полученный объем.

Пример: Вычислите объем куба со стороной 2 дюйма.
Решение: Объем куба со стороной 2 дюйма будет иметь объем (2 × 2 × 2) = 8 кубических дюймов.
Таким образом, он может вместить в общей сложности 8 кубов по 1 дюйму каждый. То же самое можно понять с помощью данной схемы.
Объем куба с использованием диагонали
Зная диагональ, мы можем выполнить шаги, указанные ниже, чтобы найти объем данного куба.
- Шаг 1: Запишите размер диагонали данного куба.
- Шаг 2: Примените формулу для нахождения объема по диагонали: [√3×(диагональ) 3 ]/9
- Шаг 3: Выразите полученный результат в кубических единицах.
Пример: Вычислите объем куба с диагональю 3 дюйма.
Решение:
Дано: Диагональ = 9 в
Мы знаем, объем куба = [√3×(диагональ) 3 ]/9
⇒ Объем = [√3×(3) 3 ]/9 = 3 × √3 = 3 × 1,732 = 5,196 в 3 .
Важные примечания:
Формулы для нахождения объема куба:
- V = s 3 , где s — длина ребра куба.
- V = √3×d 3 /9, где d — длина диагонали куба.
Задающие вопросы:
- Если стороны двух кубиков равны 8 и 12 дюймов, сколько маленьких кубиков может поместиться в больший?
- Почему отношение объемов двух кубов с отношением длин сторон 1:2 будет равно 1:8?
Объем куба Примеры
Пример 1: Используя формулу объема куба, вычислите длину стороны кубика Рубика, объем которого равен 64 в 3 .
Решение: Найти: Длина куба (s) = 4 дюйма
Дано: Объем кубика Рубика = 64 в 3
Используя формулу объема куба,
Объем куба = s 3 , где s — длина стороны.Ставим значения, получаем,
⇒ 64 = (с 3 )
⇒ с = (64) 1/3 = 4 дюймаОтвет: Длина стороны кубика Рубика = 4 дюйма
Пример 2: Найдите объем куба, если длина его диагонали равна 12 дюймам?
Решение: Найти: Объем куба
Дано: диагональ куба = 12 дюймов.
Используя формулу объема куба,
Объем куба по диагонали:
Объем куба = (√3×d 3 )/9
⇒ Объем данного куба = (√3×12 3 )/9 = 332,544 дюйма 3Ответ: Объем куба = 332,544 дюйма 3
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронировать бесплатный пробный урок
Практические вопросы по объему куба
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Volume of Cube
Что вы подразумеваете под объемом куба?
Объем куба определяется как общее пространство, ограниченное кубом в трехмерном пространстве. Он представляет собой общее количество кубических единиц, полностью занятых кубом. Объем куба помогает определить вместимость объекта кубической формы.
Объем куба помогает определить вместимость объекта кубической формы.
Как рассчитать объем куба?
Чтобы вычислить объем куба, нам нужно либо измерить длину его стороны, либо длину его диагонали.
- Чтобы найти объем, используя длину стороны куба, мы умножаем сторону трижды.
- Чтобы вычислить объем куба по диагонали, мы можем применить формулу: (√3×d 3 )/9, где d — длина диагонали тела куба.
Какова единица объема куба?
Единицей объема куба является кубическая единица или (единица измерения) 3 . Кроме того, единицей объема в СИ является кубический метр (м 3 ), который представляет собой объем, занимаемый кубом, каждая сторона которого равна 1 м. Некоторые другие важные единицы измерения: кубические футы (футы 3 ), кубические сантиметры (см 3 ), кубические миллиметры (мм 3 ), кубические дюймы (в 3 ), кубические ярды (ярды 3 ), и т. д.
д.
Какая формула объема куба?
Объем куба получается путем трехкратного умножения его стороны. Таким образом, формула объема куба может быть представлена как Объем куба = s 3 , где s — длина стороны куба.
Как найти сторону куба, зная объем?
Объем куба с использованием его стороны рассчитывается как сторона × сторона × сторона или (сторона) 3 . Эту формулу можно изменить, чтобы вычислить длину стороны как сторону = ∛Объем.
Каков объем куба со стороной 1 метр?
Чтобы найти объем куба, найдем длину стороны куба. Объем куба со стороной 1 метр = (1) 3 м 3 = 1 м 3 . Это значение представляет собой общее пространство, ограниченное данным кубом.
Как найти объем куба с помощью калькулятора?
Объем куба можно легко и быстро определить с помощью калькулятора объема куба. Это онлайн-инструмент, который помогает детям выполнять вычисления с точностью и получать ответы за считанные секунды.


 его длине, умноженной на его ширину. Что касается квадрата, так как длина и ширина равны, площадь поверхности будет «s 2 ».
его длине, умноженной на его ширину. Что касается квадрата, так как длина и ширина равны, площадь поверхности будет «s 2 ».
