Площадь окна в котельной и в частного дома
Для многоквартирных многоэтажных домов, а также для типовых проектов индивидуального строительства площадь окна в жилой комнате – параметр, просчитанный специалистами заранее, и для владельца квартиры он не имеет значения, так как уже соответствует всем нормам и стандартам. Но для застройщиков, которые возводят собственное жилье с «нуля», по собственному проекту, площадь окна – такой же важный параметр, как марка цемента или прочность бетона. Расчетная площадь остекления помогает не только сделать правильное освещение в помещении – это и правильная расстановка мебели, и правильные расчеты балки перекрытия проема, и многое другое.
Таблица расчета площади окна
Нормативы и правила
Существуют разработанные на практике и научно доказанные нормы, определяющие расчет площади окна, который влияет на остальные параметры помещения. Ниже приведены основополагающие вытяжки из нескольких СНиП для застройщиков:
- В СНиП 31-01-2003 определяются соотношения остекления к общей площади пола для кухонных и жилых помещений в доме – они должны выдерживать диапазон 1:5,5 – 1:8.
 Кроме того, здесь же указывается более широкое понимание этого параметра: в малоэтажных домах для верхних этажей с наклонным остеклением (чердаки, мансарды, террасы) соотношение светового проема окна к полу помещения должно составлять ≥ 1:10. Также площадь остекления может варьироваться в зависимости от естественного освещения и характеристик самого окна;
Кроме того, здесь же указывается более широкое понимание этого параметра: в малоэтажных домах для верхних этажей с наклонным остеклением (чердаки, мансарды, террасы) соотношение светового проема окна к полу помещения должно составлять ≥ 1:10. Также площадь остекления может варьироваться в зависимости от естественного освещения и характеристик самого окна; - В СНиП 31-02-2001 определены требования к потоку естественного света через оконные проемы в кухонных и жилых комнатах. Оптимальное значение естественного светового потока будет обеспечено соотношением остекления к площади пола как 1:8, для чердаков и мансардных помещений с наклонными окнами – как 1:10, но не меньше;
- В СНиП 2.08.01-89 и СНиП 23-05-95 нормируются требования к более многочисленной группе помещений по естественному освещению. Это жилые и кухонные помещения, санузлы без подвода канализации, коридоры и холлы, не связанные непосредственно с жилыми помещениями, лестничные клетки, коридоры и проходы в зданиях «трамвайного» типа, общественные жилые помещения.
 Во всех перечисленных помещениях соотношение остекления оконных проемов к площади пола должно быть ≤ 1:5,5 с учетом того, что минимальное соотношение допускается как 1:8, а для чердаков и мансард с наклонными окнами – 1:10.
Во всех перечисленных помещениях соотношение остекления оконных проемов к площади пола должно быть ≤ 1:5,5 с учетом того, что минимальное соотношение допускается как 1:8, а для чердаков и мансард с наклонными окнами – 1:10.
Пример быстрого расчета площади остекления
Рассчитывая площадь остекления к площади пола, отталкиваются от следующих необходимых шагов:
- Необходимо рассчитать площадь оконного проема и определить размеры переплета с тем, чтобы узнать объем светового потока и площадь остекления;
- Необходимо определиться с типоразмером и схемой оконного переплета, если нет возможности использовать стандартную схему;
- Необходимо проработать чертежи каждого окна с указанием точных размеров при невозможности применения стандартного окна.
 При этом минимальная площадь остекления регулируется светотехническими нормами – от СП 31-110-2003 до МГСН 2.06-99;
При этом минимальная площадь остекления регулируется светотехническими нормами – от СП 31-110-2003 до МГСН 2.06-99; - Соотношение остекления помещения к площади пола не должно зависеть от климатического и географического региона жилого объекта, а также от ориентировки здания по сторонам света;
- При планировке помещения с использованием окон для освещения ими второстепенных помещений дополнительным светом площадь остекления рассчитывается с учетом всех площадей помещений, которые будут освещаться этими световыми проемами.
Геометрический коэффициент при определении светового потока
Требования по световым потокам для помещения с естественным освещением, но освещаемого искусственно дополнительно, определяются площадью оконного проема, который должен быть:
- В санузлах – 0,5 от общей площади пола помещения;
- В душевых и ванных комнатах – 0,25 от общей площади пола помещения;
- В холлах, тамбурах и коридорах – 0,16 от общей площади пола помещения;
- Во входных помещениях с естественным освещением площадь проема окна может находиться в пределах 0, 4-0,5 от площади пола помещения.

Также:
- При наличии окон в длинном коридоре любое место стены напротив окна не должно находиться к окну ближе, чем на 750 см;
- Если длинный коридор освещен только окном в торце помещения, то расстояние самой дальней точки стены от окна не должно быть больше: для северных регионов 20 метров, для южных – 25 метров;
- Если коридор освещается с обеих концов естественным освещением, то его длина не должна быть более 55 метров.
Как рассчитать основные размеры окна
При проектировании жилья определяется минимальная площадь окон и место их установки. Исходя из этого, можно рассчитать более точные и конкретные параметры для каждого окна каждого помещения, чтобы узнать площадь остекления. При расчетах принято определять максимальную высоту окна для конкретного помещения, чтобы использовать оптимальные условия естественного освещения.
С учетом того, что высота подоконника – 70-90 см, а в домах с централизованным отоплением 80-90 см, а верхняя перемычка окна должна находиться не выше 15-25 см от потолка, легко просчитать максимальную высоту окна и применить к ней световое соотношение сторон – эти посчитанные параметры будут соответствовать требованиям СНиП.
Расчет высоты окна от пола и потолка
Согласно СНиП, при общей площади остекления, соответствующей 10-12% площади пола комнаты, в нее будет поступать минимальное количество естественного света. При этом оптимальной считается ширина оконного проема, соответствующая 55% от ширины комнаты.
Соотношение сторон окна играет больше визуальное значение, чем конструктивное. Также правильно выбранное соотношение сторон – это комфортность пользование фрамугами. Поэтому обычно за стандартные соотношения принимаются правильные пропорции, например, 8:13. Для расчета размеров окна существуют компьютерные программы, также можно прибегнуть и к помощи онлайн калькулятора.
Кроме того, существуют правила, которые необходимо соблюдать при проведении любых расчетов. Например, перед тем, как посчитать параметры окна и светового потока, принимается, что для одного жилого помещения угол падения естественного освещения через остекление должен быть 18-300, а площадь остекления должна лежать в диапазоне 14-17% от общей площади пола в комнате.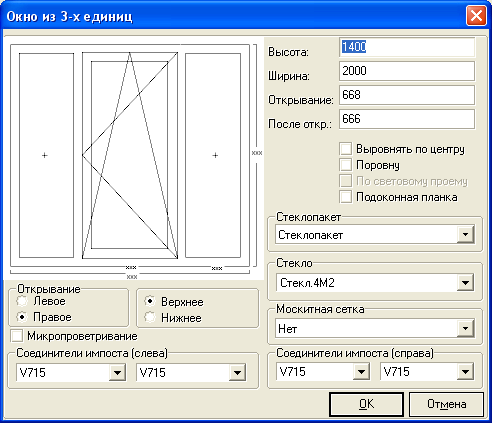
При расчете параметров необходимо учитывать соседние строения – угол падения естественного потока света зависит от высоты расположения оконного проема и близости соседствующих с жильем зданий. Естественный поток освещения будет уменьшаться при уменьшении расстояния между домами, и наоборот. Это же относится и к углу падения освещенности – чем выше близлежащие строения, тем выше угол светового потока.
Пример нахождения расчетных точек
Окно в проектировании здания считается наиболее уязвимой поверхностью с точки зрения тепло- и энергообмена, поэтому любые стандартные расчеты требуют минимизации размеров окна, что приводит к уменьшению естественного светового потока через остекленную площадь. Чтобы не возникало конфликта между желанием увеличить освещение и тепловыми потерями, составлены и действуют соответствующие СНиП. По этим же рекомендациям, коэффициентам и формулам проектировщики проводят расчеты освещенности и естественных световых потоков для разных помещений.
Расчет угла аварийного освещения
Результаты расчетов в виде соотношений сторон окна приведены ниже. Это примеры для объектов гражданского назначения, расположенных в средней полосе России на высоте ≤ 800 метров над уровнем моря, при незначительном затенении соседними объектами:
- Помещения, предназначенные для проживания, включая номера в гостинице, ресторанные и торговые помещения: 1:8-1:6;
- Помещения для приготовления пищи и коридоры: 1:10-1:8;
- Лестничные марши и клетки: 1:14-1:10;
- Учебные, детские и игровые помещения: 1:4-1:3;
- Читальные и спортивные залы: 1:6-1:5;
- Научные кабинеты и лаборатории: 1:7-1:5;
- Помещения административного управления: 1:10-1:6;
- Помещения медицинских кабинетов: 1:7-1:5;
- Помещения для больных – палаты: 1:7-1:6;
Ориентация здания по сторонам света
Но эти результаты площадей остекления и соотношения сторон проемов, рассчитанные по формулам, все же можно считать ориентировочными, так как отдельный расчет естественного освещения для каждого окна в помещении обязателен.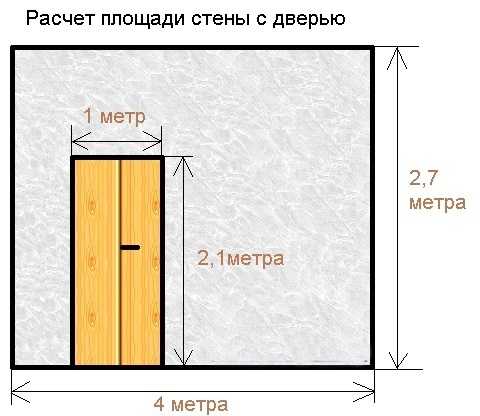
Как посчитать площадь стен
Для оценки сметы и объема закупок перед началом отделочных работ нужно знать метраж стен. Расход большинства строительных материалов (краски, штукатурки, шпаклевки) определяется площадью. Также этот параметр важен при поиске бригад, так как большинство отделочников работы оценивают по стоимости за квадратный метр.
Инструменты для измерений
- Рулетка с возможностью зафиксировать длину.
- Стальная строительная линейка.
- Уголок необходим для измерения прямого угла.
- Пузырьковый уровень полезен в тех случаях, когда нужно проверить отклонения плоскостей от горизонтали или вертикали.
- Отвес – веревка с грузом поможет отбить прямой угол. Например, это может оказаться полезным при измерении треугольных стен.
- Гидравлический или лазерный уровень поможет нанести точки на одинаковой высоте.
- Стремянка для измерения высоты.

Не обязательно иметь все эти инструменты, можно обойтись рулеткой и блокнотом для записи, но наличие дополнительного оборудования позволит получить более точные результаты.
Как рассчитать площадь прямоугольных стен
Чтобы найти площадь прямоугольника, нужно длину стены на ее высоту. Для квадрата достаточно знать длину стены по плинтусу, её нужно возвести во вторую степень. У прямоугольных помещений обычно одна стена длинная, а другая короткая, нужно установить площадь (S) этих стен по формуле.
S = (S1+S2)*2
S1 – площадь короткой стены
S2 – площадь длинной стены
Также площадь стен можно выяснить с помощью периметра (P), расчет производится по следующей формуле.
S = P*h
P – периметр пола, сумма длин всех стен.
h – высота помещения
Идеальных комнат практически не существует, поэтому для точного результата можно измерить посчитать площадь каждой стены отдельно, затем суммировать данные.
Как посчитать квадратуру стен за вычетом проемов
Предыдущие расчеты не учитывают оконные и дверные проемы. В этих зонах не будет штукатурки и обоев, поэтому их нужно вычесть. Для этого рассчитываем площадь каждого окна и двери.
В этих зонах не будет штукатурки и обоев, поэтому их нужно вычесть. Для этого рассчитываем площадь каждого окна и двери.
S = S1 – S2 – S3
S – площадь комнаты без окон и дверей
S1 – общая площадь стен
S2 – площадь окна
S3 – площадь двери
Также нужно не забывать о радиаторах, печах и каминах, а площадь оконных откосов надо, наоборот, добавить, если они будут оштукатурены. Рассчитать их можно по следующей формуле.
S (откосов) = P*a
P – периметр оконного проема
a – глубина оконного проема
Как правильно рассчитать площадь стен со сложной поверхностью
Большинство стен не представляет собой идеальный прямоугольник. В конструкциях встречаются выступы, пилястры, у потолка могут выпирать балки или перекрытия.
Определение площади помещений неправильной формы
Чтобы правильно рассчитать площадь помещения сложной конфигурации, нужно разделить их на прямоугольники, а затем результаты суммировать.
Как считать квадратные метры стен с круглыми элементами
Полукруглые выступы редко встречаются в архитектуре частных строений, но такие здания все равно есть.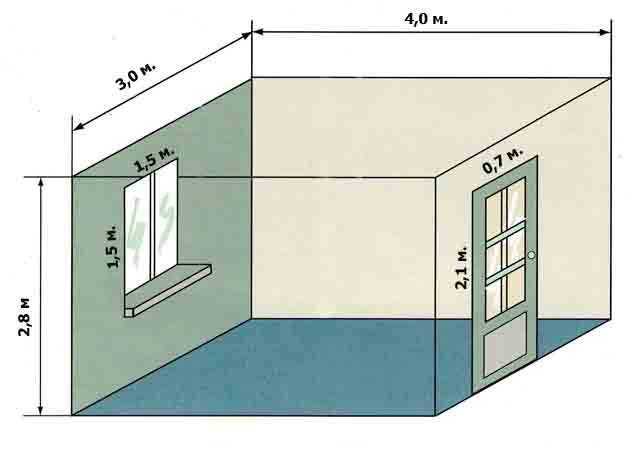 Если цилиндрический элемент выступает в виде балкона или эркера, то можно воспользоваться формулой периметра и высоты.
Если цилиндрический элемент выступает в виде балкона или эркера, то можно воспользоваться формулой периметра и высоты.
Основную часть комнаты вычисляем по формуле периметра прямоугольника, затем определяем периметр окружности и делим его пополам.
Pо = 2π*R
Pпо = Pо/2 = 2π*R/2 = π*R
Pо – периметр окружности
Pпо – периметр полуокружности
Pобщ. = A+B+A+ Pпо
S = Pобщ.*h
S = (π*R+A+A+B)*h
R – радиусом является расстояние от центра до окружности. Фактически для этого нужно измерить ширину проема и разделить это число на два.
Цилиндрические элементы не всегда имеют форму правильной окружности, в некоторых случаях требуется определить периметр эллипса или отдельного его сектора.
P = 2π√(a²+b²)/2
a, b – полуоси элипса
Затем складываем это значение с периметром стен прямоугольной части комнаты.
Если здание имеет округлый обрез кровли, то рассчитать через периметр не получится, надо отдельно вычислить площадь такой стены (в нашем случае — окна). Для этого рассчитывается площадь прямоугольника и половины круга.
Для этого рассчитывается площадь прямоугольника и половины круга.
Sпо = π*R²/2
Sпо – площадь половины круга
Sав = а*в
Sав – площадь прямоугольной части окна
S = Sпо + Sав
Как рассчитать квадратные метры конструкций в виде треугольника
Треугольных комнат не бывает, но такой силуэт может создаваться за счет наклонов скатной крыши на мансардном этаже. Сначала разбиваем стену на прямоугольную и треугольную части. Площадь треугольника считаем по формуле.
S = 0,5*a*h
a – основание треугольника AB
h – высота
Рассчитаем площадь стен на примере мансардного этажа дома с двускатной кровлей.
P = (a+b)*2
Вычисляем периметр помещения
S = P*h
Высоту считаем по стороне прямоугольника, а не по высоте до конька. Получаем площадь стен до мауэрлата.
Мауэрлат – это брус, который укладывают на стену. На него опираются стропильные ноги.
S = S1+S2*2
S1 – площадь прямоугольных участков стен
S2 – площадь треугольного участка стен до стропил.
Расчет будет отличаться для дома с односкатной крышей. Такие типы кровель часто встречаются на пристройках и гаражах. В этом случае площадь между стропилами и линией мауэрлата высчитывается по формуле для прямого треугольника.
S = 0,5*a*b
a – длина ската до стены.
b – высота стены от крыши до линии мауэрлата.
Как рассчитать квадратные метры конструкций в виде трапеции
У вальмовой крыши обрез кровли образует не треугольник, а трапецию. В этом случае расчет надо производить по следующей формуле.
S = (a+b)/2*h
a – ширина верхней части стены.
b – ширина стены на уровне мауэрлата.
h – высота стены до линии мауэрлата от верхней точки.
Объем помещения
Знание площади стен позволяет узнать объем помещения. Эта информация помогает для расчета отопительных и вентиляционных систем.
Если комната имеет форму параллелепипед, то объем высчитывается через произведение ширины, длины и высоты.
V = S*h
S – площадь пола.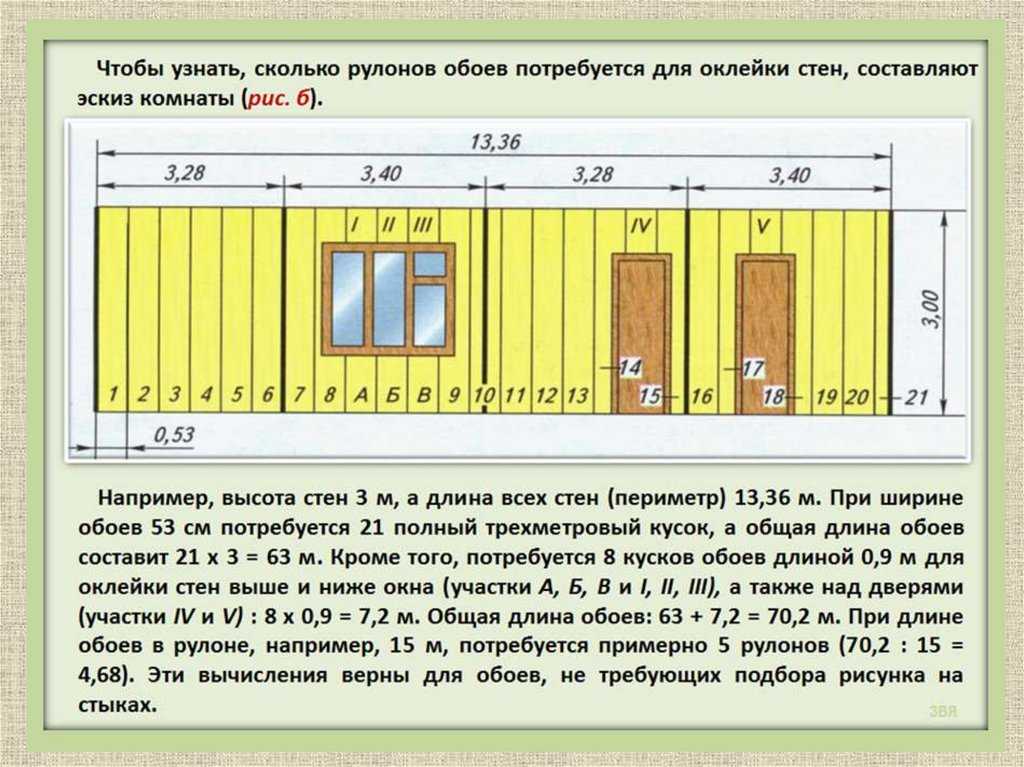
h – высота комнаты.
В комнате с двухскатной крышей нужно сначала рассчитать площадь подкровельного пространства, которое имеет форму призмы.
V = S*h
h – высота призмы, в нашем случае это длина комнаты, перпендикулярная стене с фронтоном.
S – площадь фронтона.
Советы и рекомендации
- Учитывайте неровности стен. Вертикали и горизонтали в многоквартирных домах часто отклоняются от идеальных показателей. В этом случае лучше брать среднюю величину, а замеры производить рядом с плинтусами и в центральной части.
- Для отметки ровных осей будет полезен лазерный уровень.
- Если не удается определить периметр сложной конструкции, то вдоль плинтуса можно уложить веревку. Затем ее распрямляют и измеряют.
- Для измерения вертикалей используйте отвес: веревку с грузом закрепляют на самой высокой точке, затем ее можно снять и измерить. Отвес всегда показывает перпендикуляр к линии горизонта.
Вычисление площади | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры.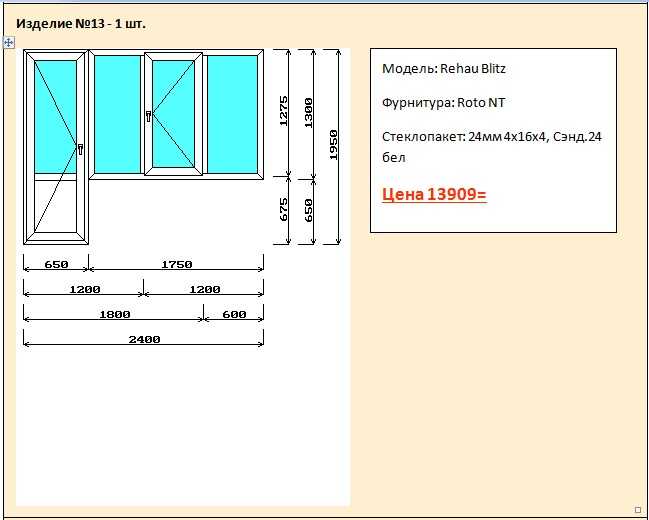 Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади методом сетки
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».
Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике квадратные сантиметры сокращаются до см 2 . 2 означает «квадратный».
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не вписывается точно в сетку.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 полных квадратов сетки (заштрихованы синим цветом).

- 10 половинных квадратов сетки (заштрихованы желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
- Также есть 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.
Следовательно, площадь этого квадрата равна 30,25 см 2 .
Вы также можете записать это как 30¼cm 2 .
Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.
Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.
Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.
Площади простых четырехугольников:
Квадраты, прямоугольники и параллелограммы
Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Площадь прямоугольника = высота × ширина
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длина в квадрате.
Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.
Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.
Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.
Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.
Другая распространенная проблема заключается в том, чтобы найти область границы — фигура внутри другой фигуры.
В этом примере показан путь вокруг поля шириной 2 метра.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете представить путь как четыре отдельных прямоугольника, вычислить их размеры, затем их площадь и, наконец, сложить площади вместе, чтобы получить общую сумму.
Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.
- Площадь всей фигуры 16 м × 10 м = 160 м 2 .

- Мы можем рассчитать размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
- Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
- То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
- Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.
- Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м 2 .
- Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м 2 .
Площадь пути 88 м 2 .
A Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины. Прямоугольник по определению является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой подразумевается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .
Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Вычисление площади треугольников
Треугольник можно представить как половину квадрата или параллелограмма.
Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро определить его площадь, используя следующую формулу:
Площадь треугольника = (высота × ширина) ÷ 2.
Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.
Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь вычисляется:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника равна 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:
Вы хотите покрасить фронтон сарая. Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере размеры:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует некоторых дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.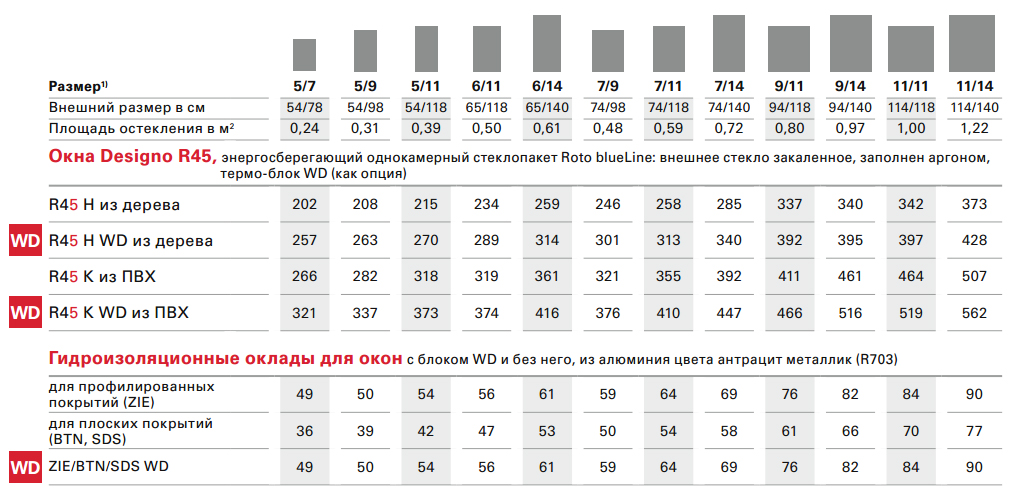
Размер D = 12,4 – 6,6
D = 5,8 м
Теперь можно вычислить площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2
Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две площади вместе, чтобы найти общую площадь:
76,56 + 33,64 м = 1100
Как известно, один литр краски покрывает 10 м 2 стены, чтобы мы могли вычислить, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 литра.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
Площади кругов
Для вычисления площади круга необходимо знать его диаметр или радиус .
Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус окружности — это длина прямой линии от центральной точки окружности до ее края. Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.
На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.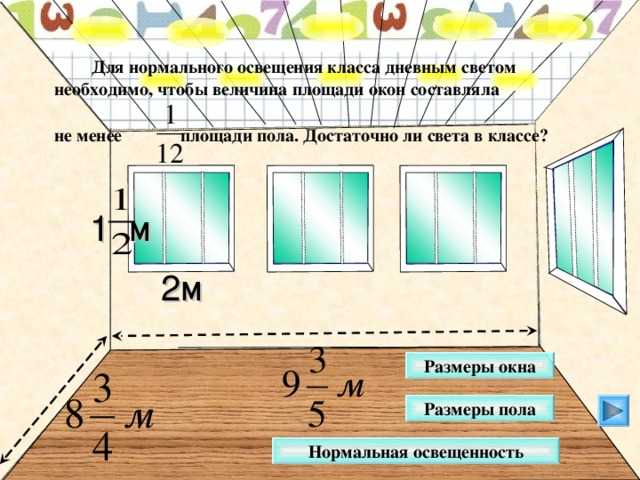
Радиус нужен для вычисления площади круга, формула такова:
Площадь круга = πR 2 .
Это означает:
π = Pi — константа, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3,142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3м имеет площадь:
Сначала вычисляем радиус (3м ÷ 2 = 1,5м)
Затем применяем формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м равна 7,0695 м 2 .
Заключительный пример
Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).
Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:
| А – 9,7 м | В – 7,6 м |
| С – 8,8 м | Г – 4,5 м |
| В – 2,3 м | В – 2,7 м |
| Г – 1,2 м | В – 1,0 м |
Примечания:
- Все измерения являются приблизительными.
- О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
- Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.
- Размер круглого окна — это диаметр окна.
- Размеры двери включают ступени.
Какова площадь деревянной решетчатой части дома?
Вычисления и ответы ниже:
Ответы на приведенный выше пример
Сначала вычислите площадь основной формы дома – прямоугольника и треугольника, составляющих фигуру.
Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м 2 .
Высота треугольника (A – B) 9,7 – 7,6 = 2,1.
Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.
Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м 2 .
Пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м 2 .
Затем добавьте площади дверей и окон.
(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из полной площади.
76,12 – 27,3355 = 48,7845
Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. нашу страницу по Оценка, приближение и округление .
Инструкция по измерению
Инструкция по измерению
|
| ДОМ По вопросам об окне |

 Кроме того, здесь же указывается более широкое понимание этого параметра: в малоэтажных домах для верхних этажей с наклонным остеклением (чердаки, мансарды, террасы) соотношение светового проема окна к полу помещения должно составлять ≥ 1:10. Также площадь остекления может варьироваться в зависимости от естественного освещения и характеристик самого окна;
Кроме того, здесь же указывается более широкое понимание этого параметра: в малоэтажных домах для верхних этажей с наклонным остеклением (чердаки, мансарды, террасы) соотношение светового проема окна к полу помещения должно составлять ≥ 1:10. Также площадь остекления может варьироваться в зависимости от естественного освещения и характеристик самого окна; Во всех перечисленных помещениях соотношение остекления оконных проемов к площади пола должно быть ≤ 1:5,5 с учетом того, что минимальное соотношение допускается как 1:8, а для чердаков и мансард с наклонными окнами – 1:10.
Во всех перечисленных помещениях соотношение остекления оконных проемов к площади пола должно быть ≤ 1:5,5 с учетом того, что минимальное соотношение допускается как 1:8, а для чердаков и мансард с наклонными окнами – 1:10. При этом минимальная площадь остекления регулируется светотехническими нормами – от СП 31-110-2003 до МГСН 2.06-99;
При этом минимальная площадь остекления регулируется светотехническими нормами – от СП 31-110-2003 до МГСН 2.06-99;





 Мы будем
Мы будем