Сообщающиеся сосуды — законы, принципы, формулы
Жидкое агрегатное состояние
Давайте для начало разберемся, как ведет себя жидкость в различных сосудах.
В мире есть три агрегатных состояния: твердое, жидкое и газообразное.
Их характеристики — в таблице:
Агрегатные состояния | Свойства | Расположение молекул | Расстояние между молекулами | Движение молекулы |
|---|---|---|---|---|
Твердое | сохраняет форму и объем | в кристаллической решетке | соотносится с размером молекул | колеблется около своего положения равновесия в кристаллической решетке |
Жидкое | сохраняет объем и текучесть | хаотично | близко друг к другу | малоподвижны, при нагревании скорость движения молекул увеличивается |
Газы | занимают весь предоставленный объем | хаотично | больше размеров молекул | хаотичное и непрерывное |
В этом состоянии сохраняется объем, но не сохраняется форма. Например, если перелить молоко из кувшина в стакан — молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.
Например, если перелить молоко из кувшина в стакан — молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.
Расстояние между молекулами в жидком состоянии чуть больше, чем в твердом, но все равно невелико. При этом частицы не собраны в кристаллическую решетку, а расположены хаотично. Молекулы почти не двигаются, но при нагревании жидкости делают это более охотно.
Вспомните, что происходит, если залить чайный пакетик холодной водой — он почти не заваривается. А вот если налить кипяточку — чай точно будет готов.
Агрегатных состояния точно три? На самом деле, есть еще четвертое — плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором помимо нейтральных частиц, есть еще и заряженные. |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Сообщающиеся сосуды
Поскольку жидкость принимает форму сосуда, в который ее поместили, имеет место быть такое явление, как сообщающиеся сосуды.
- Сообщающиеся сосуды — это сосуды, соединенные между собой ниже уровня жидкости (в каждом сосуде). Так жидкость может перемещаться из одного сосуда в другой.
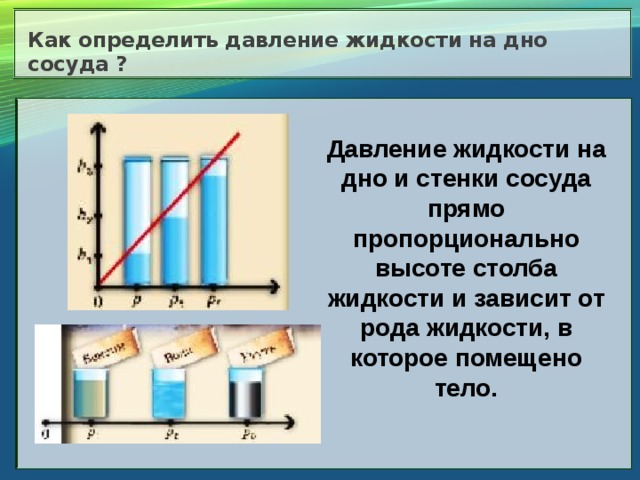
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Если в колена сообщающихся сосудов налить жидкости, плотности которых будут различны, то меньший объём более плотной жидкости в одном колене уравновесит больший объём менее плотной жидкости в другом колене сосуда.
Другими словами, высота столба жидкости с меньшей плотностью больше, чем высота столба жидкости с большей плотностью. Давайте рассчитаем, во сколько высота столба жидкости с меньшей плотностью больше высоты столба жидкости с большей плотностью, если эти две несмешивающиеся жидкости находятся в сообщающихся сосудах.
p = ρgh, p1 = p2, ρ1 gh1= ρ2 gh2,
Отсюда:
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Применение сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости — ареометра. Этот прибор состоит из двух сообщающихся сосудов: двух вертикальных стеклянных трубок, соединенных между собой третьей изогнутой трубкой.
Одна из вертикальных трубок заполняется жидкостью, плотность которой нужно определить, а другая — жидкостью известной плотности (например, водой, плотность которой равна 1000 кг/м3). Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).
Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).
Также на законе сообщающихся сосудах основаны устройства, которые определяют уровень жидкости в закрытых сосудах: резервуарах, паровых котлах.
Чтобы судно могло переплыть из одной водного бассейна в другой, если уровни воды в них разные, необходимо использовать шлюз. Устройство шлюза также основано на принципе сообщающихся сосудов. В первых воротах шлюза открывается клапан, камера соединяется с водоёмом, они становятся сообщающимися сосудами, уровни воды в них выравниваются. После этого ворота открываются, и судно проходит в первую камеру. Открывается следующий клапан, после выравнивания уровней воды открываются ворота, и так повторяется столько раз, сколько камер имеет шлюз.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Давление столба жидкости
Выведем формулу давления столба жидкости через основную формулу давления.
Давление p = F/S p — давление [Па] F — сила [Н] S — площадь [м2] |
В случае давления жидкости на дно сосуда мы можем заменить силу в формуле на силу тяжести.
Также мы можем представить массу жидкости как произведение плотности на объем:
Из геометрии мы знаем, что объем тела вращения (например, цилиндра) — это произведение площади основания на высоту: V = Sh.
Следовательно, высота будет равна h = V/S. Подставляем в формулу высоту вместо отношения объема к площади.
В сообщающихся сосудах давление жидкости на одном уровне (на одной и той же высоте) будет одинаковым.
А можно сделать так, чтобы давление было разным? С помощью перегородки можно сделать так, чтобы уровень жидкости, а следовательно, и давления в сообщающихся сосудах отличались. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем дополнительное давление. Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд, где её уровень ниже — до тех пор, пока высота жидкости в обоих сосудах не станет одинаковой. Этот принцип используют в водонапорной башне. |
Задачка
Какой площади необходимо сделать малый поршень в гидравлическом прессе, для того, чтобы выигрыш в силе получился равным 2? Площадь большого поршня равна 10 см2.
Решение:
Гидравлический пресс — это два цилиндрических сообщающихся сосуда. Площадь большого поршня, с приложенной силой F1, равна 10 см2.
Площадь малого поршня обозначим Sмал, к нему приложена сила F2.
Давления в сообщающихся сосудах на одинаковой высоте равны: p1 = p2
Подставим формулу давления:
F1 / Sбол = F2 / Sмал.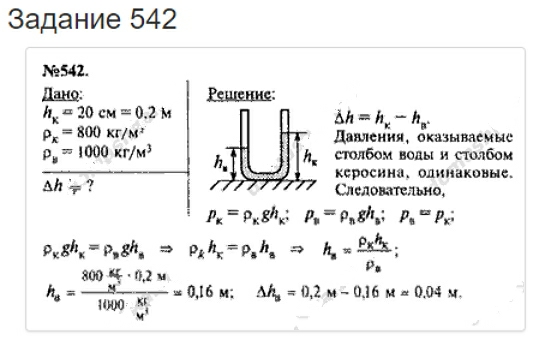
Выразим Sмал, получим:
Sмал = (F2 / F1) · Sбол
Так как по условию выигрыш в силе F2 / F1 равен 2, то:
Sмал = 2 · Sбол = 2 · 10 = 20 см2
Ответ: малый поршень необходимо сделать с площадью равной 20 см2
Расчёт давления жидкости на дно и стенки сосуда
Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда». ВЫ УЗНАЕТЕ: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда. ВСПОМНИТЕ: Как формулируется закон Паскаля? Как определить давление твёрдого тела на опору? Как зависит масса тела от его плотности? Что такое вес тела? Как вес тела зависит от его массы?
Конспекты по физике Учебник физики Тесты по физике
Жидкость, находящаяся в сосуде, оказывает давление как на дно сосуда, так и на его стенки. Поверхность жидкости, которая не соприкасается со стенками сосуда, называют свободной поверхностью жидкости. Давление, оказываемое покоящейся жидкостью, называют гидростатическим.
Поверхность жидкости, которая не соприкасается со стенками сосуда, называют свободной поверхностью жидкости. Давление, оказываемое покоящейся жидкостью, называют гидростатическим.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА ДНО СОСУДА
Вычислим давление жидкости на дно сосуда площадью S, если высота столба жидкости в этом сосуде равна h. Как известно, давление определяется по формуле p = F/S.
В нашем случае сила F, с которой жидкость действует на дно сосуда, равна её весу. Вес жидкости определяется по формуле Р = mg. (1)
Следовательно, для определения веса жидкости необходимо найти её массу. Для этого воспользуемся формулой m = pV, где р — плотность жидкости, а V — объём жидкости. Для определения объёма необходимо найти произведение площади дна сосуда и высоты столба жидкости: V = Sh.
Следовательно, масса жидкости в сосуде определяется по формуле m = рSh. (2)
Подставим это выражение в формулу (1) и получим Р = gpSh. (3)
Теперь для нахождения давления необходимо вес жидкости разделить на площадь сосуда: P = gpSh/S
Сократив в полученном выражении S в числителе и знаменателе, получим формулу для расчёта давления жидкости на дно сосуда: p = pgh. (4)
Давление жидкости на дно сосуда рассчитывают по формуле p = pgh.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА СТЕНКИ СОСУДА
Так как по закону Паскаля давление внутри жидкости на одном и том же уровне одинаково по всем направлениям, то по формуле (4) можно находить давление жидкости на стенки сосуда на любой глубине.
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда прямо пропорционально высоте столба жидкости и зависит по только от высоты столба жидкости, но и от плотности жидкости р. Чем больше плотность жидкости, тем большее давление она оказывает при условии, что высота столба жидкости остаётся постоянной.
Даже при использовании дыхательных трубок, выступающих над водой, глубина погружения человека не может превышать 1,5 м, так как из-за давления воды у него не хватает сил увеличив объём грудной клетки и вдохнуть воздух. В 1943 г французами Ж. Кусто и Э. Ганьяном был изобретён акваланг специальный аппарат со сжатым воздухом, предназначенный для дыхания под водой и позволяющий находиться под водой от нескольких минут (на глубине около 40 м) до часа и более.
В соответствии с формулой (4) давление жидкости также зависит от ускорения свободного падения g. Значит, если представить себе один и тот же сосуд с жидкостью, помещенный на разные планеты, то давление на дно и стенки сосуда в нем будет различно в зависимости от значения g на планете.
ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости и не зависит от формы сосуда.
Приведённая схема опыта показывает, что сила, с которой жидкость оказывает давление на дно сосудов различной формы, но с одинаковой площадью дна и одинаковой высотой столба жидкости в них, будет одной и той же. Каждый из сосудов снабжён съемным дном, и динамометры показывают именно 3 силу воздействия воды на дно сосудов, но не вес жидкости. Очевидно, что вес жидкости в сосудах будет различным, так как объёмы жидкости в сосудах неодинаковы.
По закону Паскаля давление столба жидкости высотой h равномерно передаётся в любую точку дна каждого из сосудов. Именно поэтому сила, с которой жидкость оказывает давление на дно, больше веса жидкости в сосуде В, но меньше веса жидкости в сосуде С. Несмотря на кажущееся противоречие, ничего парадоксального в этих опытах нет.
Несмотря на кажущееся противоречие, ничего парадоксального в этих опытах нет.
ОПЫТ ПАСКАЛЯ
Даже небольшим количеством воды можно создать очень большое давление. В 1648 г. этот факт очень убедительно продемонстрировал В. Паскаль, поразив своих современников. В прочную, наполненную водой и закрытую со всех сторон бочку площадью поверхности 2 м2 была вставлена тоненькая трубочка площадью сечения 1 см2 и высотой 5 м. Затем Паскаль поднялся на балкон второго этажа и влил в эту трубочку всего кружку воды. Из-за малого диаметра трубки вода поднялась до большой высоты, и давление на стенки бочки так возросло, что планки (клёпки) бочки разошлись и вода стала вытекать из бочки.
Вы смотрели Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда»: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда.
Вернуться к Списку конспектов по физике (В оглавление).
Объяснение урока: Жидкостный манометр
В этом объяснении мы научимся описывать процесс давления
измерение по высоте столба жидкости в U-образной трубке.
Жидкостный манометр представляет собой U-образную трубку, заполненную жидкостью, которая используется для
измерить разность давлений газов по обе стороны от него. Манометр открыт
в атмосферу, заполненную водой, показано ниже.
Уровень воды одинаков с обеих сторон трубы. В связи с этим давление на
левая сторона, 𝑃L, равна давлению на правой стороне,
𝑃R (т.е. когда высота воды на обоих
левая и правая стороны равны, поэтому и давление):
𝑃=𝑃LR
когда
ℎ=ℎ.LR
Если одна сторона трубки подключена к давлению, отличному от атмосферного,
тогда высота жидкости может измениться, как показано на диаграмме ниже.
Неизвестный газ и атмосфера оказывают давление на жидкость,
но теперь давление другое, поэтому высота воды по бокам
трубка имеет разницу, Δℎ.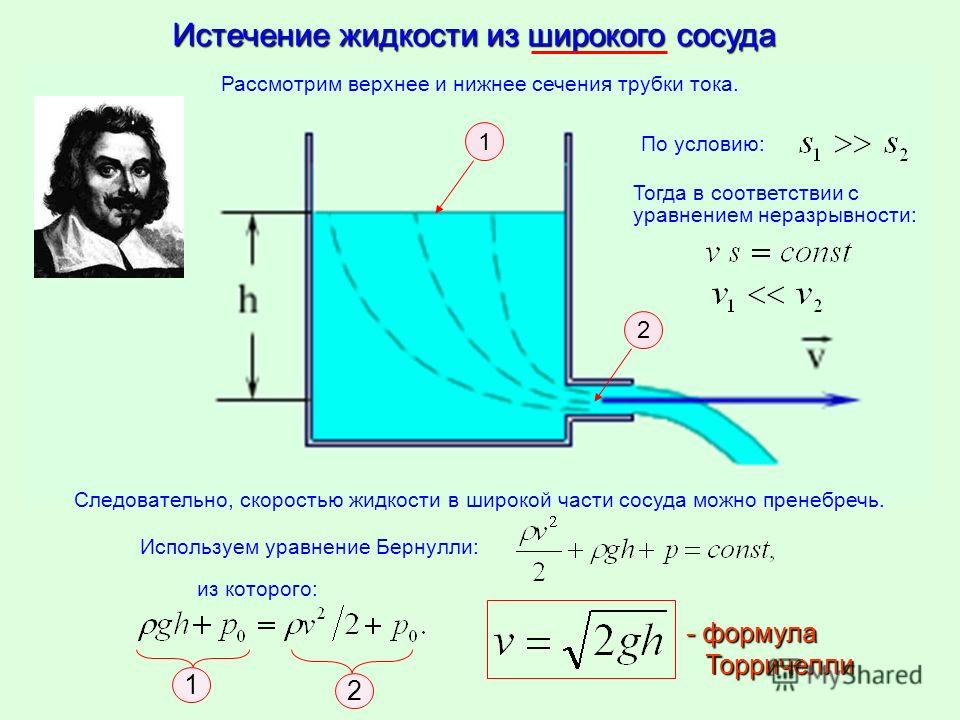
Если ℎR больше, чем ℎL, то это означает
на воду давит меньше; таким образом, 𝑃R есть
менее 𝑃L:
𝑃>𝑃LR
когда
ℎℎLR
наоборот.
Давайте рассмотрим несколько примеров.
Пример 1. Сравнение жидкостного манометра с неизвестным газом
На схеме показан жидкостный манометр, подключенный одним концом к
газовый резервуар и на противоположном конце в атмосферу. Что из следующего правильно относится к давлению
газа и атмосферного давления,
𝑃газ и 𝑃атм?
- 𝑃>𝑃газатм
- 𝑃𝑃газатм
- 𝑃=𝑃газатм
Ответ
𝑃газ давление с правой стороны, поступающее
из газового резервуара. 𝑃атм это давление на
левая сторона, исходящая из атмосферы.
Если 𝑃gas больше, чем
𝑃атм, то высота жидкости в
манометр будет смещен вверх влево. Если 𝑃атм
вместо этого было больше, чем 𝑃атм, то это было бы
подтолкнул вверх вправо.
Так как высота одинаковая, значит и давление с обеих сторон одинаковое. Правильный ответ C, 𝑃=𝑃газатм.
Пример 2: Неравномерное сравнение жидкостного столбового манометра с неизвестным газом
На схеме показан жидкостный манометр, подключенный одним концом к
газовый резервуар и на противоположном конце в атмосферу. Какое из следующих утверждений правильно относится к давлению газа
и давление атмосферы, 𝑃газ
и 𝑃атм? ответ
из газового резервуара. 𝑃атм — давление на
левая сторона, исходящая из атмосферы.
Поскольку высота столба жидкости в трубке различна, мы знаем, что
𝑃gas не может быть равно
𝑃атм. Они разные, поэтому один должен быть больше
чем другой.
Если бы 𝑃атм было больше, то жидкость в колонке
толкнули бы вверх вправо, но жидкости там нет выше; это
ниже. Следовательно, 𝑃gas должно быть больше, чем
𝑃атм.
Таким образом, правильный ответ B, 𝑃>𝑃gasatm.
Пропорция, на которую отличается давление, связана с высотой
разница. Большая разница в высоте означает большую разницу в давлении. Мы можем использовать модифицированную версию уравнения для давления в колонне, чтобы выразить
это.
Уравнение: изменение давления жидкостного манометра
Уравнение, используемое для связи изменения давления с изменением высоты
в манометре есть
Δ𝑃=𝜌𝑔Δℎ,
где Δ𝑃 — разница давлений,
𝜌 — плотность жидкости, 𝑔 — сила
из-за гравитации
(9,81 м/с 2 для
Земля), а Δℎ — разница высот.
Из этого уравнения видно, что Δ𝑃 пропорционально
Δℎ. Двойное изменение высоты означает двойное изменение
под давлением.
Давайте решим задачу, использующую это отношение. Жидкостный манометр
содержит воду, плотность которой примем за
997 кг/м 3 . Левая сторона соединена с газом неизвестного давления, а правая
сторона открыта в атмосферу на уровне моря, которую мы примем за
101,3 кПа.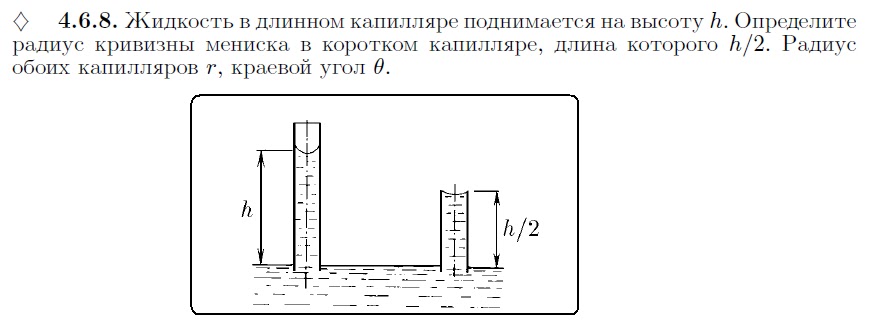 Мы также можем принять гравитацию как
Мы также можем принять гравитацию как
9,81 м/с 2 .
Ищем неизвестное давление газа с левой стороны. Давайте возьмем
посмотрите на уравнение изменения давления в столбе:
Δ𝑃=𝜌𝑔Δℎ.
Важно отметить, что нас интересует только величина изменения высоты,
так что это не может быть отрицательным.
Точно так же разница в давлении также является величиной. Выраженная сама собой,
это может выглядеть
Δ𝑃=|𝑃−𝑃|RL
или же
Δ𝑃=|𝑃−𝑃|.LR
Мы знаем, что из-за меньшей высоты жидкости,
𝑃>𝑃LR. Это означает
что мы можем принять вторую форму без абсолютного значения, так как знаем, что это
будь позитивным.
Это делает уравнение похожим на
𝑃−𝑃=𝜌𝑔Δℎ.LR
Нам нужен 𝑃L с одной стороны, поэтому давайте добавим 𝑃R к обеим сторонам, чтобы изолировать его:
𝑃−𝑃+𝑃=𝜌𝑔Δℎ+𝑃𝑃=𝜌𝑔Δℎ+𝑃.LRRRLR
𝑃R — атмосфера на уровне моря,
101,3 кПа. Другой
значения 𝜌 как
997 кг/м 3 , 𝑔 as
9,81 м/с 2 , и
Δℎ как
10 см. Перед тем, как вставить
Перед тем, как вставить
Δℎ, переведем в метры, помня
что в нем 100 см
метр:
11001100×10=0,1.мкммсмсм
Итак, 10 см это
0,1 м. Ввод их в уравнение дает
𝑃=997/9,81/(0,1)+(101,3).LkgmmsmkPa
В правой части счетчики частично компенсируют друг друга, чтобы стать
1/м 3 указано по плотности. Подстановка цифр дает
𝑃=978×+(101.3).LkgmskPa
Нам нужно, чтобы единицы справа совпадали, прежде чем мы сможем их добавить
вместе. Напомним, что паскали
ньютонов на квадратный метр
/Нм и что
Ньютоны
килограмм-метр в секунду в квадрате
⋅/кгм. Мы можем преобразовать единицы, которые у нас есть, в ньютоны на квадратный метр следующим образом:
кгmskgmsmkgmsmNm×=×1×1=,
составим наше уравнение
𝑃=978+(101.3).LPakPa
Сделаем единицы измерения паскалей одинаковыми. Есть
1 000 Па в 1 кПа:
11000,11000×978=0,978.kPaPakPaPaPakPa
Сложение их вместе дает
𝑃=0,978+(101,3)𝑃=(102,278).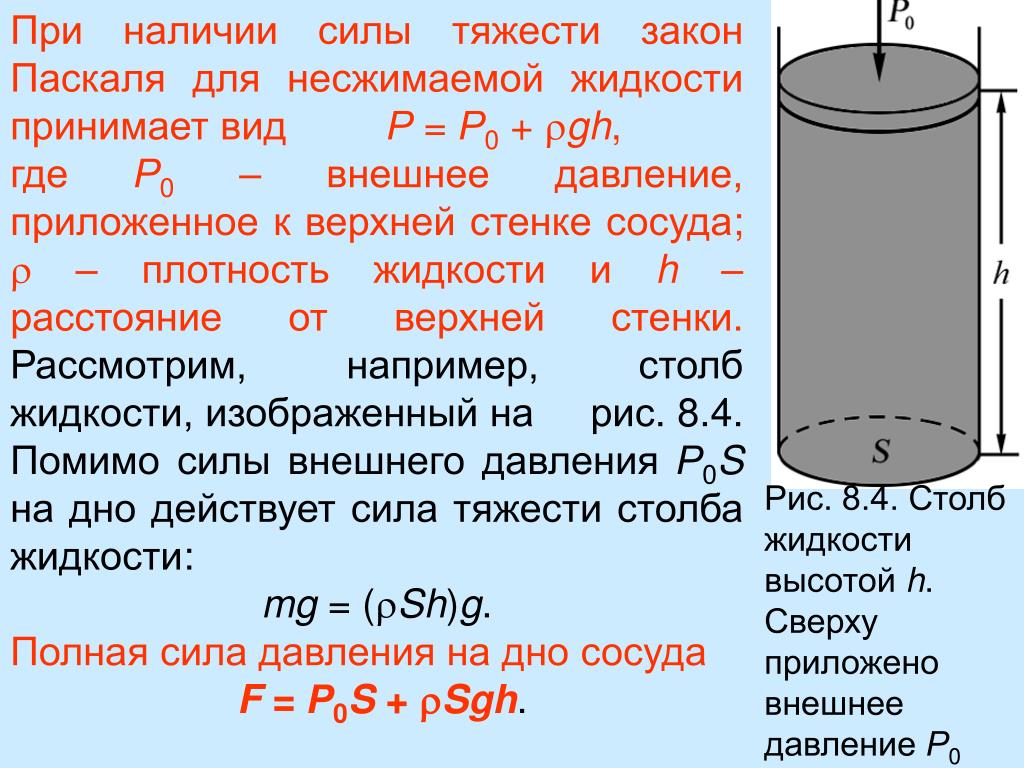 LLPakPakPa
LLPakPakPa
Округляя, неизвестное давление с левой стороны равно
102,3 кПа, а
небольшая разница. Иногда для наблюдения используются более плотные жидкости.
более резкие изменения давления.
Давайте рассмотрим пример.
Пример 3: Жидкостный манометр Расчет давления газа
На схеме показан жидкостный манометр, подключенный одним концом к газовому резервуару
а на противоположном конце в атмосферу. U-образная трубка содержит ртуть,
плотностью 13 595 кг/м 3 . Верх ртутного столба в контакте
с атмосферой находится вертикально ниже вершины ртутного столба в контакте
с газовым резервуаром. Расстояние по вертикали между вершинами колонн
ℎ=25см. Найдите давление газа в резервуаре. Используйте значение
𝑃=101,3кПа для атмосферного
давление.
- 33 кПа
- 68 кПа
- 101 кПа
- 105 кПа
- 135 кПа
изменение высоты к изменению давления между резервуаром и
сторона, открытая в атмосферу.

Рассмотрим изменение давления в уравнении столба жидкости:
Δ𝑃=𝜌𝑔Δℎ.
Мы должны найти давление газового резервуара, в дальнейшем
𝑃, а мы уже знаем 𝑃. Глядя на жидкие высоты,
тот, что открыт в атмосферу, ниже, поэтому
𝑃>𝑃. Таким образом, изменение давления будет иметь вид
Δ𝑃=𝑃−𝑃.
Возвращая это к уравнению,
𝑃−𝑃=𝜌𝑔Δℎ.
Нам нужно 𝑃 с одной стороны, поэтому добавим его к обеим сторонам:
𝑃−𝑃+𝑃=𝜌𝑔Δℎ+𝑃𝑃=𝜌𝑔Δℎ+𝑃.
Затем мы можем вычесть 𝜌𝑔Δℎ с обеих сторон, чтобы изолировать
𝑃:
𝑃−𝜌𝑔Δℎ=𝜌𝑔Δℎ+𝑃−𝜌𝑔Δℎ𝑃−𝜌𝑔Δℎ=𝑃.
Плотность известна,
13 595 кг/м 3 , сила тяжести,
9,81 м/с 2 , и
Δℎ,
25 см. Давайте сначала конвертируем
сантиметров до
метров, поэтому все единицы одинаковы:
1100×25=0,25 мкм см
Затем мы можем подставить наши известные значения в уравнение:
𝑃−13595/9,81/(0,25)=𝑃. kgmmsm
kgmmsm
Умножение вместе дает
𝑃−(33341)×=𝑃.kgms
Единицы для этого недавнего расчета преобразуются в
паскалей () ньютонов на квадратный метр, или
Па (Н/м 2 ), следующим образом:
кгmskgmsmkgmsmNm×=×1×1=,
составление уравнения
𝑃−(33341)=𝑃.Па
Давление для левой стороны, 𝑃, было задано в
килопаскаль,
поэтому давайте также преобразуем значение справа в это:
11000×33341=33,3 кПаПаПакПа
𝑃 дается как
101,3 кПа. Ставим
это и решить, чтобы получить
101,3−(33,3)=68,kPakPakPa
Таким образом, давление в газовом резервуаре равно B,
68 кПа.
Иногда необходимо найти не неизвестное давление, а неизвестное
высота. Если даны давления, мы можем найти высоту.
Глядя только на уравнение
Δ𝑃=𝜌𝑔Δℎ.
Мы можем изолировать Δℎ, разделив обе части на
𝜌𝑔:
Δ𝑃𝜌𝑔=𝜌𝑔Δℎ𝜌𝑔,
отменив правую сторону дать
Δ𝑃𝜌𝑔=Δℎ.
Точно так же, как изменение давления, нам нужно определить, как упорядочить высоты
чтобы не было негативных изменений. Например, на приведенной ниже диаграмме можно
ясно видно, что ℎR больше, чем ℎL.
Таким образом, изменение высоты будет выглядеть как
Δℎ=ℎ−ℎ,RL
хотя обычно требуется только изменение высоты.
Давайте рассмотрим пример.
Пример 4: Расчет разницы высот жидкостного манометра
На схеме показан жидкостный манометр, соединенный противоположными концами с двумя газовыми
водохранилища. Давление в газовых резервуарах
𝑃=123,3кПа
и 𝑃=110,1кПа. В U-образной трубке находится масло плотностью
1 080 кг/м 3 . Каково вертикальное расстояние ℎ между вершинами масляных столбов? Дайте ответ с точностью до двух знаков после запятой.
- 22,05 м
- 12,22 м
- 11,65 м
- 1,25 м
- 0,62 м
90
Δℎ:
Δ𝑃=𝜌𝑔Δℎ.
Мы можем получить Δℎ само по себе, разделив обе части на
𝜌𝑔:
Δ𝑃𝜌𝑔=𝜌𝑔Δℎ𝜌𝑔,
который становится
Δ𝑃𝜌𝑔=Δℎ.
Значение Δ𝑃 представляет собой разницу между давлениями
𝑃 и 𝑃. Мы хотим, чтобы он был положительным, поэтому, поскольку
𝑃>𝑃, изменение давления выглядит как
Δ𝑃=𝑃−𝑃.
𝑃 составляет 123,3 кПа и
𝑃 составляет 110,1 кПа,
означает, что изменение давления равно
123,3−110,1=13,2.kPakPakPa
Поскольку мы получим окончательный ответ в метрах, мы хотим
килопаскаль,
кПа, чтобы быть в
паскаль,
Па. 1 000 Па в
килопаскаль:
1000110001×13,2=13200.PakPaPakPakPaPa
Теперь у нас есть все переменные, необходимые для определения изменения высоты. Плотность
1 080 кг/м 3
а 𝑔 равно 9,81 м/с 2 . Таким образом, уравнение выглядит как
13200(1080/)(9.81/)=Δℎ. Пакгмм
Пакгмм
Нам нужно связать единицы
паскаль к
килограммы,
метров и
секунды. Единицы паскаля
ньютонов на квадратный метр
/Нм,
а ньютоны
килограмм-метров в секунду в квадрате. Вместе преобразование выглядит так
Nmkgmsmkgmsmkgms=×1×1=×.
Объединение всех этих единиц дает
13200(1080)(9.81)××××=Δℎ.kgmsmskgm
Сокращением единиц в числителе с единицами в
знаменатель, единицы значительно упрощаются до метров:
13200(1080)(9,81)=Δℎ.м
Затем мы упрощаем, чтобы дать
Δℎ=1,2458.m
Учитывая два десятичных знака, ответ, таким образом, D, 1,25 м.
Давайте подытожим то, что мы узнали из этого объяснения.
Ключевые моменты
- Уравнение, используемое для связи изменения давления и изменения высоты
жидкостный манометр
Δ𝑃=𝜌𝑔Δℎ.
где Δ𝑃 — разница давлений,
𝜌 — плотность жидкости,
𝑔 — сила тяжести, а
Δℎ — разница в высоте.
- В жидкостном манометре коэффициент изменения высоты равен
коэффициент изменения давления.
Давление
Давление
Давление в статической жидкости зависит от веса жидкости и выражается выражением
Давление от веса столба жидкости площадью А и высотой h равно Самое замечательное в этом выражении то, что оно Из-за простоты визуализации высоты столба известной жидкости стало обычной практикой указывать все виды давления в единицах высоты столба, таких как мм рт. с точки зрения высоты столба жидкости. Расчет | Индекс Расчет давления жидкости Концепции давления | ||
| Назад |
|

 Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.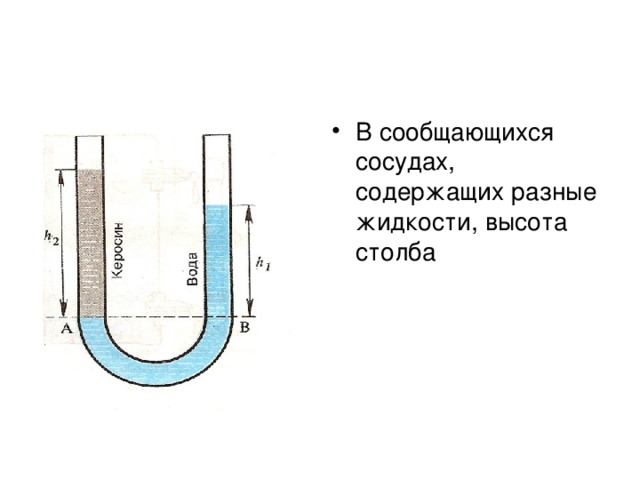 Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.
Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.
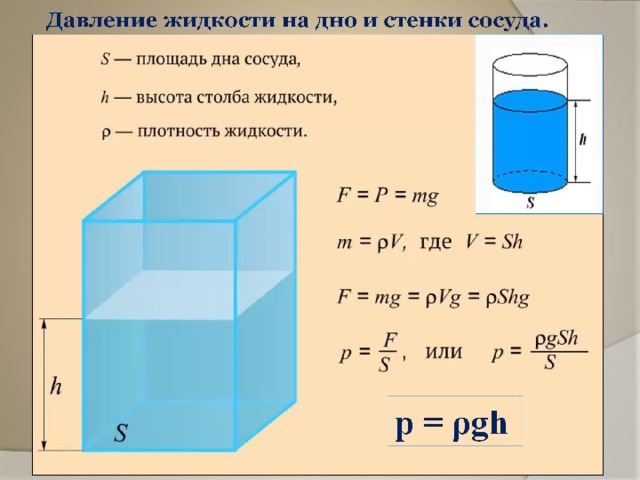 Приведенное выше выражение давления легко увидеть для
Приведенное выше выражение давления легко увидеть для