кубатурник

производство пиломатериала

Главная > кубатурник

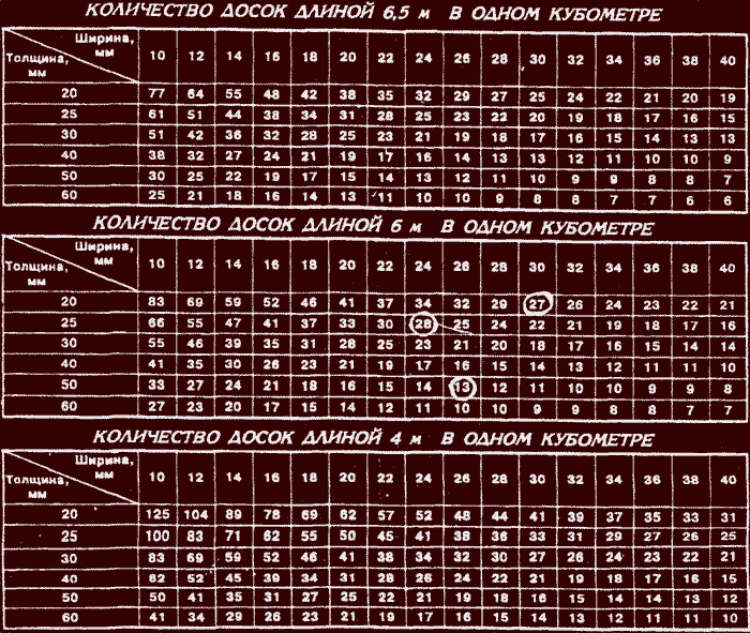
Используя данную таблицу, Вы всегда с легкостью сможете перевести штуки в кубы и обратно, узнать сколько штук бруса или доски в кубе, вес, объём, количество погонных метров в кубе. В таблице приведены основные размеры изделий.

6.

2 Связанные курсы

Пример 6.2.5
Качели состоят из доски на конце веревки длиной 10 футов. Подумайте о
доске как точка $P$ на конце веревки, а $Q$ — точка
крепление на другом конце. Предположим, что свинг находится прямо под $Q$
в момент времени $t=0$, и его толкает кто-то, кто идет в 6
футов/сек слева направо. Найдите: а) как быстро растет колебание после 1
сек; б) угловая скорость каната в град/с через 1 с.

Начнем с вопроса: что такое геометрическая
величина, скорость изменения которой нам известна, и какова геометрическая величина
о чьей скорости изменения нас спрашивают? Обратите внимание, что человек, толкающий
качели движутся горизонтально с известной нам скоростью. Другими словами,
горизонтальная координата $P$ увеличивается со скоростью 6 футов/сек. в
$xy$-плоскость позволяет сделать удобный выбор, поместив начало координат в
положение $P$ в момент времени $t=0$, т.е. на расстоянии 10 непосредственно под точкой
привязанности. Тогда известная нам скорость равна $dx/dt$, и частично
(a) желаемая скорость равна $dy/dt$ (скорость, с которой растет $P$). Частично
(b) желаемая скорость равна $\ds \dot{\theta}=d\theta/dt$, где $\theta$ означает
угол в радианах, на который качели отклонились от вертикали.
(На самом деле, поскольку мы хотим получить ответ в град/сек, в конце мы должны преобразовать
$d\theta/dt$ из рад/сек путем умножения на $180/\pi$.)
92=100$. Взяв производную от обеих частей, получим:
$2x\dot{x}+2(10-y)(0-\dot{y})=0$. Теперь посмотрим на то, что мы знаем после 1
во-вторых, а именно $x=6$ (поскольку $x$ начинается с 0 и увеличивается в
скорость 6 футов/сек за 1 секунду), $y=2$ (потому что мы получаем $10-y=8$ из
теорема Пифагора применяется к треугольнику с гипотенузой 10 и
ветвь 6) и $\ds \dot{x}=6$. Ввод этих значений дает нам
$2\cdot 6\cdot 6-2\cdot 8\dot{y}=0$, откуда легко решить
для $\ds \dot{y}$: $\ds \dot{y}=4,5$ фут/сек.

(b) Здесь у нас две переменные $x$ и $\theta$, поэтому мы хотим использовать
тот же прямоугольный треугольник, что и в части (а), но на этот раз свяжите $\theta$ с
$х$. Поскольку гипотенуза постоянна (равна 10), лучший способ
сделать это, чтобы использовать синус: $\sin\theta=x/10$.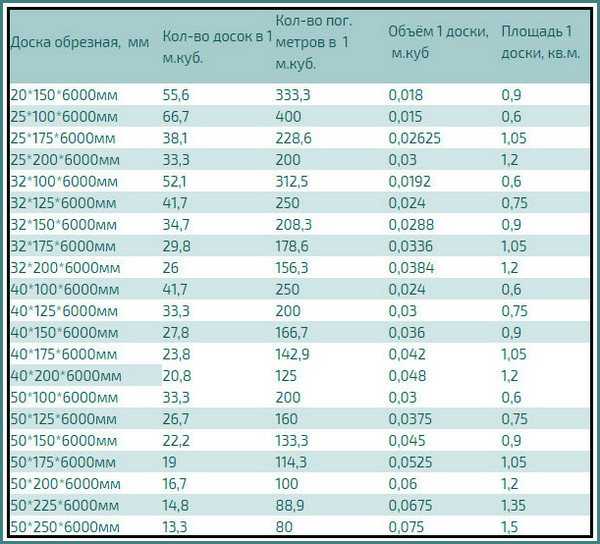 Взяв производные, мы
получить $\ds (\cos\theta)\dot{\theta}=0,1\dot{x}$. В данный момент в
вопрос ($t=1$ сек), когда у нас есть прямоугольный треугольник со сторонами
6–8–10, $\ds \cos\theta=8/10$ и $\ds \dot{x}=6$. Таким образом
$(8/10)\dot{\theta}=6/10$, т. е. $\ds \dot{\theta}=6/8=3/4$ рад/сек, или
примерно $43$ град/сек.
$\квадрат$

Мы видели, что иногда их явно больше двух.
переменных, которые изменяются со временем, но на самом деле их всего две, т.к.
остальные могут быть выражены только двумя. Но иногда там
действительно есть несколько переменных, которые меняются со временем; до тех пор, как вы
зная скорости изменения всех, кроме одного из них, вы можете найти скорость
изменения оставшегося. Как в случае, когда есть только два
переменных, возьмите производную от обеих частей уравнения, связывающего все
переменные, а затем подставить все известные значения и решить для
неизвестная ставка.

Пример 6.2.6
Дорога, идущая с севера на юг, пересекает дорогу, идущую с востока на запад.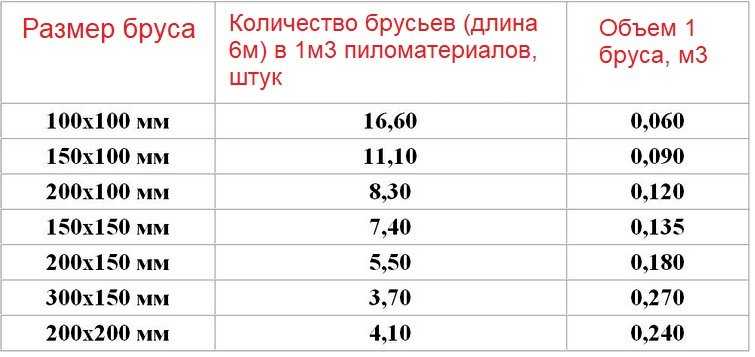 2}}={460\over\sqrt{13}} \ приблизительно 127,6 \hbox{км/ч}
$$
на момент интереса.
$\квадрат$

Обратите внимание, чем эта задача отличается от примера 6.2.2. В обоих случаях мы начали с теоремы Пифагора и
взял деривативы с обеих сторон. Однако в
пример 6.2.2 одна из сторон была константой
(высота самолета), и поэтому производная квадрата
эта сторона треугольника была просто нулевой. В этом примере на
С другой стороны, все три стороны прямоугольного треугольника являются переменными, даже
хотя нас интересует конкретное значение каждой стороны
треугольник (а именно, когда стороны имеют длины 10 и 15). Убедись в том, что
вы понимаете в начале задачи, что такое переменные и
какие константы.
93$/сек?
(отвечать)

Пример 6.2.2
Цилиндрический резервуар, стоящий вертикально (с одним круглым основанием на
земля) имеет радиус 1 метр. С какой скоростью поднимается уровень воды в
падение бака при сливе воды со скоростью 3 литра в секунду?
(отвечать)

Пример 6.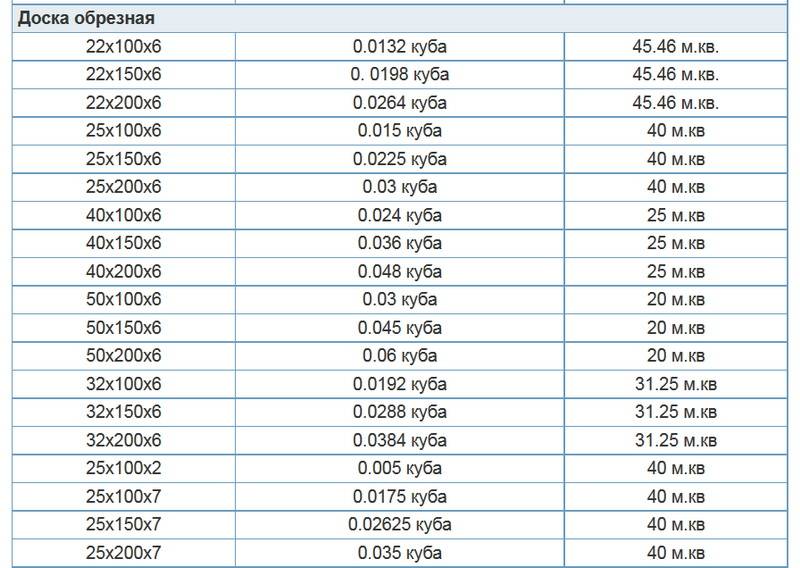 2.3
Лестница длиной 13 м опирается на горизонтальную поверхность и наклоняется.
у вертикальной стены. Ножка лестницы отодвинута от
стены со скоростью 0,6 м/сек. Как быстро верх сползает вниз
стены, когда основание лестницы находится на расстоянии 5 м от стены?
(отвечать)

Пример 6.2.4
Лестница длиной 13 м опирается на горизонтальную поверхность и наклоняется.
у вертикальной стены. Верх лестницы поднимается вверх
стены со скоростью $0,1$ метра в секунду.
С какой скоростью приближается подножие лестницы
стены, когда основание лестницы находится на расстоянии 5 м от стены?
(отвечать)

Пример 6.2.5
Вращающийся маяк расположен в 2 милях от воды. Пусть $A$ будет
точку на берегу, ближайшую к маяку. Поскольку маяк вращается в
10 об/мин, луч света скользит по берегу каждый раз, когда он вращается.
Предположим, что берег прямой. С какой скоростью движется точка, в которой луч
ударяется о берег, двигаясь в тот момент, когда луч освещает точку 2
миль вдоль берега от точки $A$?
(отвечать)
93$/сек, формируя
коническая свая, диаметр основания которой всегда равен ее высоте. 3$/мин, как быстро
уровень воды повышается при увеличении глубины воды (в самой глубокой точке)
4 м? Примечание: объем любой «конической» формы (включая
пирамиды) составляет $(1/3)(\hbox{высота})(\hbox{площадь основания})$.
(отвечать)

Пример 6.2.11
Солнце восходит со скоростью $1/4$ град/мин и, кажется,
подняться в небо перпендикулярно
горизонт, как показано на рисунке 6.2.5.
С какой скоростью движется тень от 200-метрового здания
сжимается в тот момент, когда длина тени составляет 500 метров?
(отвечать)

Пример 6.2.12
Солнце садится со скоростью $1/4$ град/мин и кажется
опускаться перпендикулярно горизонту, как показано на рис.
рисунок 6.2.5. Как быстро тень 25
метровое удлинение стены в тот момент, когда длина тени составляет 50 метров?
(отвечать)
9\circ$ в секунду?
(отвечать)

Рисунок 6.2.6. Впадина.

Пример 6.2.14
Женщина ростом 5 футов идет со скоростью 3,5 фута в секунду от уличного фонаря.
это 12 футов над землей. С какой скоростью кончик ее тени
движущийся? С какой скоростью удлиняется ее тень?
(отвечать)

Пример 6. 2.15
Человек ростом 1,8 метра ходит со скоростью 1 метр в секунду.
второй к уличному фонарю, который находится на высоте 4 метров над землей. В
с какой скоростью движется кончик его тени? С какой скоростью его тень
сокращение?
(отвечать)

Пример 6.2.16
Полицейский вертолет летит со скоростью 150 миль в час на постоянной высоте 0,5 мили.
над прямой дорогой. Пилот использует радар, чтобы определить, что встречный
машина находится на расстоянии ровно 1 мили от вертолета, и что это
расстояние уменьшается со скоростью 190 миль в час. Найдите скорость автомобиля.
(отвечать)

Пример 6.2.17
Полицейский вертолет летит со скоростью 200 километров в час в
постоянной высоте 1 км над прямой дорогой. Пилот использует
радар для определения того, что встречная машина находится на расстоянии ровно 2
километров от вертолета, и что это расстояние уменьшается на 250
км/ч Найдите скорость автомобиля.
(отвечать)
92$ и через 6 секунд после машины А
стартовавший автомобиль B прошел мимо $P$, двигаясь на восток с постоянной скоростью 60 м/с.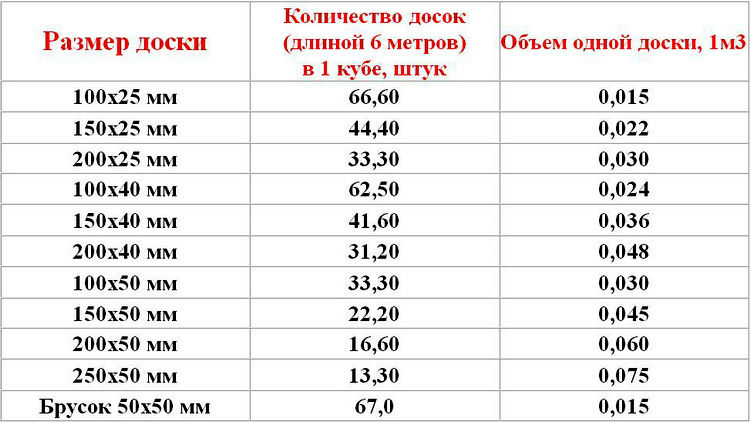
(отвечать)

Пример 6.2.22
Снова ссылаясь на пример 6.2.6,
предположим, что вместо автомобиля В летит самолет со скоростью $200$
км/ч к востоку от $P$ на высоте 2 км, как показано на рис.
рисунок 6.2.8. Как быстро проходит расстояние между
меняется машина и самолет?
(отвечать)

Рисунок 6.2.8. Автомобиль и самолет.

Пример 6.2.23
Снова обратимся к примеру 6.2.6, предположим,
что вместо машины В летит самолет со скоростью $200$
км/ч к востоку от $P$ на высоте 2 км, и что
набирает высоту со скоростью 10 км/ч.
Как быстро
расстояние между автомобилем и самолетом меняется?
(отвечать)
92/2$. Как быстро тень объекта
двигаться по земле на секунду позже?
(отвечать)

Пример 6.2.25
Два лезвия ножниц закреплены в точке $A$ как
показано на рисунке 6.2.9. Позволять
$a$ обозначает расстояние от $A$ до кончика лезвия (точки $B$).
Обозначим через $\beta$ угол при вершине лопасти, образованный
линия $\ds \overline{AB}$ и нижняя кромка лезвия, линия
$\ds ​​\overline{BC}$, и пусть $\theta$ обозначает угол между
$\ds ​​\overline{AB}$ и горизонтали.
Предположим, что лист бумаги разрезан таким образом, что центр
ножниц в $A$ фиксируется, и бумага также фиксируется. Как
лопасти сомкнуты (т.е. угол $\theta$ на диаграмме уменьшен),
расстояние $x$ между $A$ и $C$ увеличивается, разрезая бумагу.
9\circ$, найти скорость (в
см/сек), с которой режется бумага.
(отвечать)

Рисунок 6.2.9. Ножницы.

Q2 Крышка прямоугольной коробки со сторонами 40 см на 10 см обклеена лентой по всему периметру. Что нужно…

Перейти к

• Упражнение 10.1
• Упражнение 10.2
• Упражнение 10.3

• Зная наши цифры
• Целые числа
• Игра с числами
• Основные геометрические идеи
• Понимание элементарных форм
• Целые числа
• Фракции
• Десятичные
• Обработка данных
• Измерение
• Алгебра
• Соотношение и пропорция
• Симметрия
• Практическая геометрия

Главная >

Решения НЦЭРТ
Класс 6
Математика
>

Глава 10 — Измерение
>

Упражнение 10.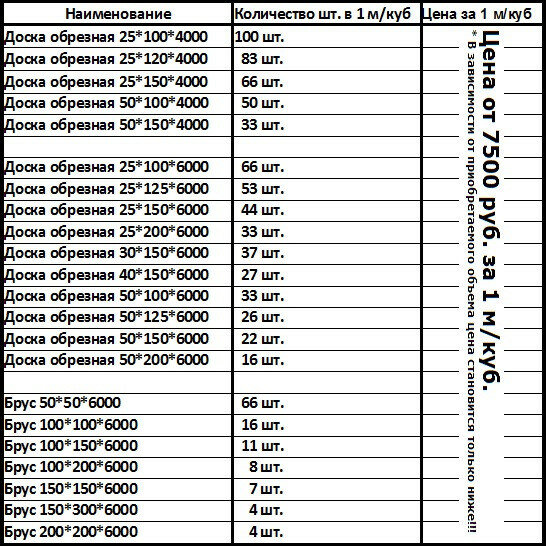 1
>
Вопрос 4

Вопрос 4 Упражнение 10.1

Q2) Крышка прямоугольной коробки со сторонами 40 см на 10 см заклеена лентой по всему периметру. Какая длина ленты требуется?

Ответ:

Решение:

Общая длина требуемой ленты = Периметр прямоугольника cmn

= 1 метр

Следовательно, необходимая общая длина ленты составляет 100 см или 1 метр.

Стенограмма видео

привет всем меня зовут нинту джейкоб я
репетитор в Лидо
и приветствую всех вас в небольшом обучении
так что это вопрос mcq вопрос
из главы нервная система
так вопрос такой ставь галочку
отметка
против правильной альтернативы и
Следующие утверждения
хорошо, так что первое утверждение
пахнущая жалкая середина продолговатого
контролирует
запах сердцебиения и
дыхательное движение
интеллект и сила воли уравновешивают
тело
Итак, мы знаем, что продолговатый металл контролирует
непроизвольные действия
так что из этого непроизвольного действия
биение сердца
дыхательное движение правильно так правильно
ответ
средние продолговатые контролируют биение
сердце и дыхательные движения
теперь второй баланс тела
контролируется
спинной мозг мозжечок головной мозг
и снова мозг
Балансировка тела является функцией которого
часть мозга
мозжечок теперь третий запах хорошей еды
вызывает слезотечение
естественный рефлекс
приобретенный рефлекс в связи рефлекс обычный
рефлекс это тип рефлекторного действия
и это приобретенный рефлекс
теперь третий или четвертый последний
один
структурно-функциональная единица
нервная система
аксон нефрон нейрон
и текстиль, который является функциональной единицей
структурно-функциональная единица
да это нейрон
Хорошо, я надеюсь, вы поняли это, если
у тебя есть сомнения
в этих ответах, пожалуйста, прокомментируйте ниже
и не забудь подписаться на
канал для получения регулярных обновлений
встретимся в следующий раз с новым
видео а пока следите за обновлениями будьте осторожны
и пока

Связанные вопросы

Q1) Найдите периметр каждой из следующих фигур: (a) (b) (c) (d) (e) (f)

Найдите периметр каждой из следующих фигур:

Крышка прямоугольной коробки со сторонами 40 см на 10 см заклеена скотчем по всему периметру.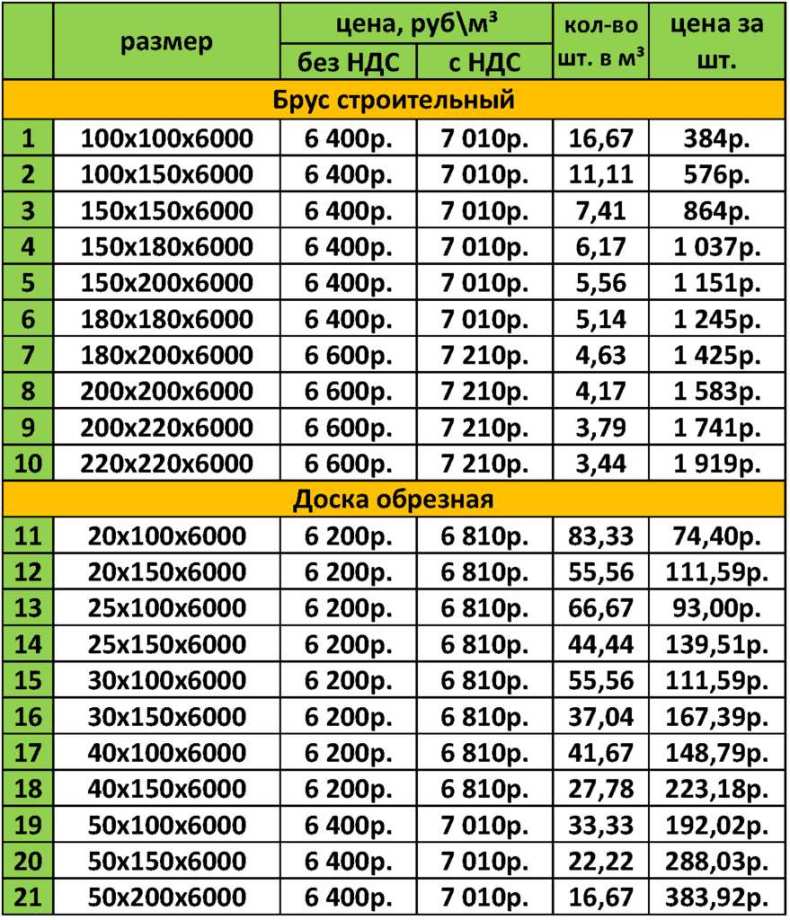 Что такое лен…

Q3) Размеры столешницы 2 м 25 см на 1 м 50 см. Каков периметр столешницы?

Размеры столешницы 2 м 25 см на 1 м 50 см. Каков периметр столешницы?

Какой длины должна быть деревянная планка, чтобы поставить в рамку фотографию длиной и шириной 32 см и…

Фейсбук

WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 10.1

Упражнение 10.2

Упражнение 10.3

Главы

Знание наших чисел

Целые числа

Игра с числами

Основные геометрические идеи

Понимание элементарных форм

Целые числа

Фракции

Десятиц

Обработка данных

Mensuration

Algebra

Ratio и Proportion

Symmetry

Symmetry

Symmetry

Symmetry

Symmetry

Symmetry

.